Multiple Compatibility for Polyaboloes
Introduction
A set of polyforms is compatible
if there exists a figure that each of them can tile.
Here are minimal figures that can be tiled by a given number of
n-aboloes.
If you find a smaller solution or one that can be tiled by more
n-aboloes, please write.
For polyominoes see Multiple Compatibility
for Polyominoes.
For polyiamonds see Multiple Compatibility
for Polyiamonds.
For polyhexes see Multiple Compatibility
for Polyhexes.
Diaboloes
2 Diaboloes
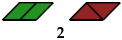
Triaboloes
2 Triaboloes
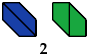
3 Triaboloes
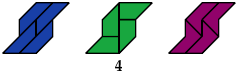
Tetraboloes
3 Tetraboloes
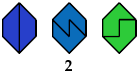
5 Tetraboloes

Pentaboloes
6 Pentaboloes

7 Pentaboloes
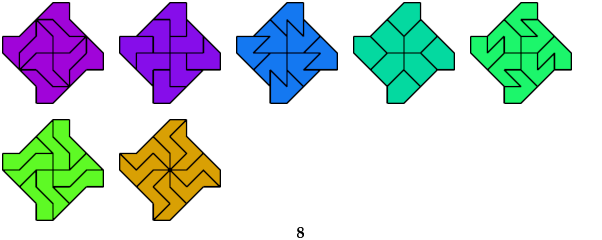
Hexaboloes
7 Hexaboloes

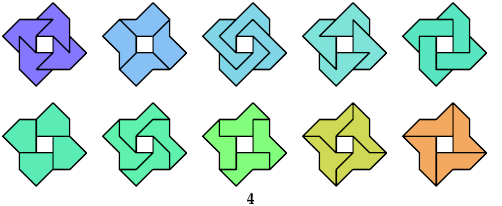
10 Hexaboloes
Last revised 2014-10-29.
Back to Multiple Compatibility
<
Polyform Compatibility
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]







