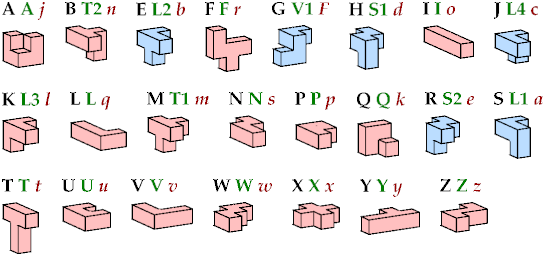

A compatibility figure for two or more polyforms is a figure that can be tiled with any of them. In 2004, Livio Zucca published Pentomino Odd Pairs, showing minimal known compatibility figures for every pair of pentominoes, using an odd number of each.
Here I show minimal known compatibility figures for every pair of pentacubes, using an odd number of each. A prime mark (′) after a letter denotes a mirror image. For example, S′ is the mirror image of S. To see a tiling, click on the corresponding entry in the table below. Missing entries indicate unsolved cases. If you solve an unsolved case, or find a smaller solution than one given here, please write.
See also Pentacube Compatibility.
| A | B | E | E′ | F | G | G′ | H | H′ | I | J | J′ | K | L | M | N | P | Q | R | R′ | S | S′ | T | U | V | W | X | Y | Z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 3 | 3 | 9 | 3 | 3 | 21 | 3 | 3 | 3 | 7 | 5 | 5 | 3 | 5 | 3 | 9 | 5 | 9 | 9 | 7 | 3 | 7 | |||||||
| B | 3 | 3 | 3 | 3 | 5 | 3 | 5 | 3 | 3 | 3 | 3 | 3 | 3 | 5 | 3 | 5 | 3 | 5 | 5 | 3 | 5 | ||||||||
| E | 3 | 3 | 3 | 3 | 3 | 3 | 15 | 3 | 3 | 3 | 5 | 5 | 3 | 3 | 3 | 3 | 3 | 5 | 5 | 5 | 5 | 3 | 5 | 9 | 3 | 5 | |||
| F | 3 | 3 | 5 | 3 | 5 | 3 | 5 | 3 | 3 | 3 | 3 | 5 | 5 | 5 | 5 | 5 | 7 | 3 | 5 | ||||||||||
| G | 3 | 3 | 5 | 15 | 3 | 3 | 3 | 3 | 5 | 3 | 5 | 3 | 3 | 3 | 3 | 5 | 7 | 9 | 3 | 7 | 25 | 5 | 5 | ||||||
| H | 3 | 9 | 3 | 3 | 3 | 3 | 7 | 3 | 3 | 3 | 3 | 3 | 5 | 3 | 5 | 3 | 5 | 3 | 9 | 3 | 5 | ||||||||
| I | 3 | 15 | 3 | – | 5 | 5 | 7 | 13 | 11 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | |||||||||||||
| J | 3 | 3 | 3 | 5 | 3 | 3 | 3 | 3 | 3 | 5 | 5 | 3 | 3 | 3 | 5 | 9 | 3 | 3 | |||||||||||
| K | 5 | 7 | 9 | 3 | 3 | 3 | 3 | 3 | 3 | 7 | 5 | 15 | 3 | 3 | |||||||||||||||
| L | 9 | 3 | 3 | 3 | 5 | 3 | 3 | 3 | 3 | 5 | 23 | 3 | 3 | ||||||||||||||||
| M | 7 | 3 | 3 | 3 | 9 | 7 | 9 | 9 | 7 | 3 | 5 | 7 | |||||||||||||||||
| N | 3 | 3 | 3 | 3 | 5 | 5 | 3 | 3 | 15 | 3 | 7 | ||||||||||||||||||
| P | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 7 | 3 | 3 | |||||||||||||||||||
| Q | 3 | 3 | 7 | 3 | 3 | 3 | 17 | 3 | 5 | ||||||||||||||||||||
| R | 3 | 3 | 3 | 5 | 5 | 7 | 3 | 9 | 3 | 3 | |||||||||||||||||||
| S | 3 | 3 | 3 | 7 | 5 | – | 3 | 3 | |||||||||||||||||||||
| T | 3 | 7 | 9 | 17 | 3 | 9 | |||||||||||||||||||||||
| U | 7 | 9 | – | 5 | 11 | ||||||||||||||||||||||||
| V | 9 | – | 5 | 7 | |||||||||||||||||||||||||
| W | 19 | 5 | 5 | ||||||||||||||||||||||||||
| X | 5 | 15 | |||||||||||||||||||||||||||
| Y | 5 | ||||||||||||||||||||||||||||
| Z | |||||||||||||||||||||||||||||
Last revised 2022-02-24.