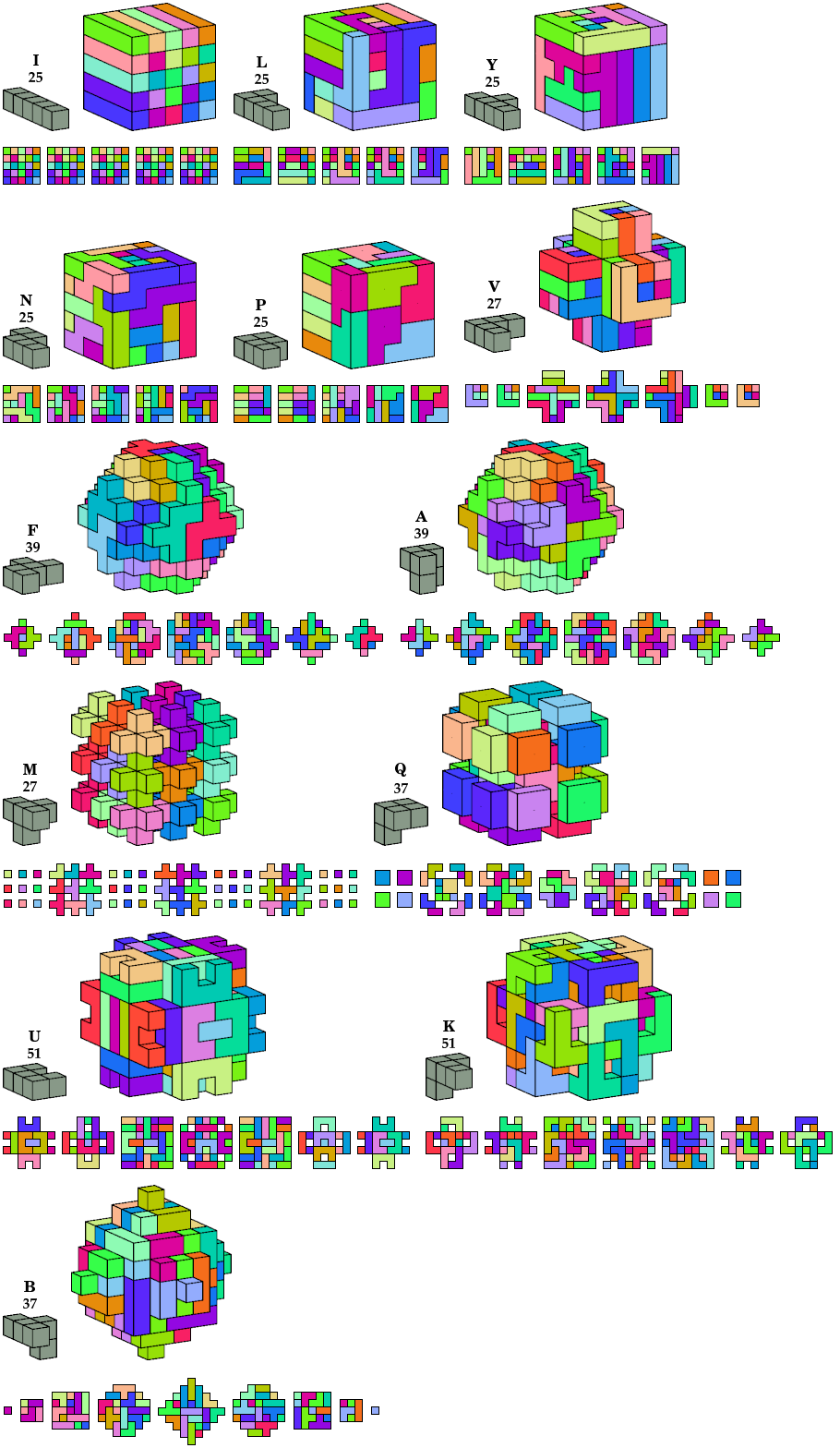
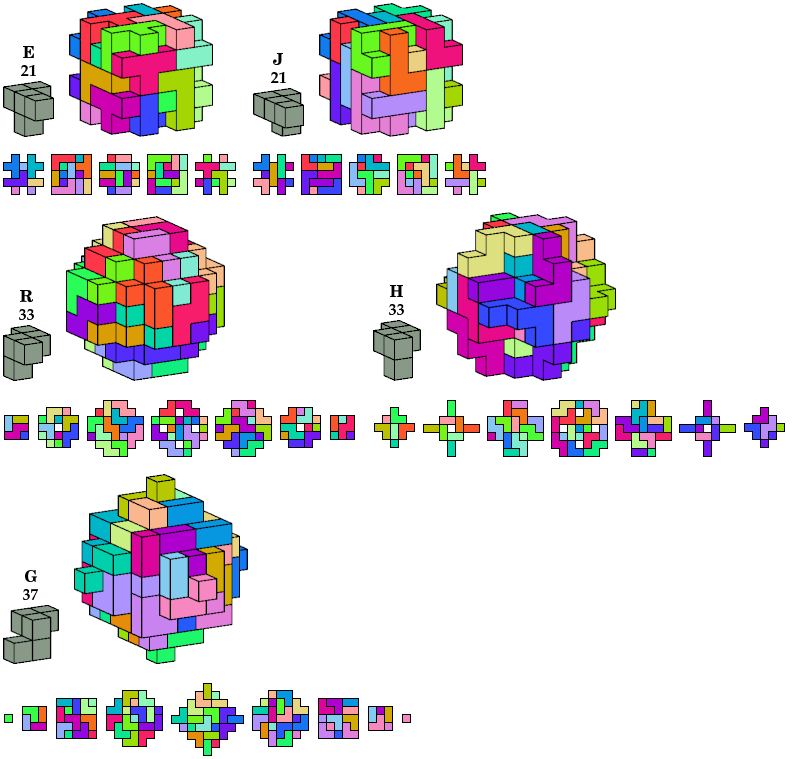
Polycubes have 33 symmetry classes (including asymmetry), and 31 of them have even order. That is too many to show here. Instead I show only oddities with full cubic symmetry.
For other classes of symmetry, see:
In all pictures, the cross-sections are shown from back to front.
Thanks to Jaap Scherphuis for pointing out an error in one of my chiral tilings.
The 5×5×5 cubes are due to Torsten Sillke.
The oddity for the B pentacube can also be tiled by the Q pentacube.

| Pentacube | Boxes | Shape | Tiles |
|---|---|---|---|

| 3×12×25
3×13×25 6×8×25 7×8×25 | 25×25×25 cube | 3125 |
 |
5×5×14
5×5×19 | 3D cross with arms 5×5×14 | 445 |
 |
5×9×25 5×16×25 | 25×25×25 cube | 3125 |
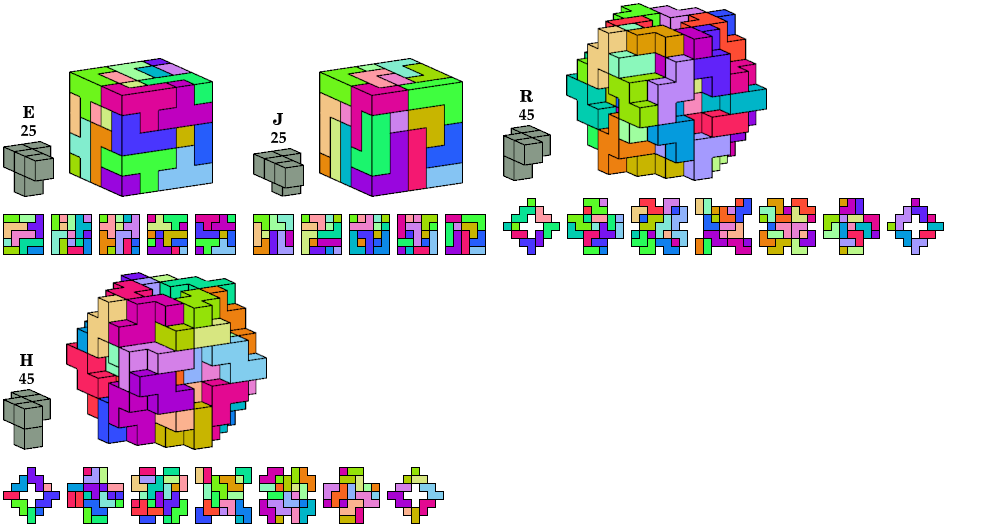
| Pentacube | Boxes | Cube | Tiles |
|---|---|---|---|

| 5×9×15
6×6×15 6×9×15 | 15×15×15 | 675 |
| Pentacube | Boxes | Cube | Tiles |
|---|---|---|---|
 | 3×5×9 5×5×6 | 15×15×15 | 675 |
Last revised 2024-03-07.