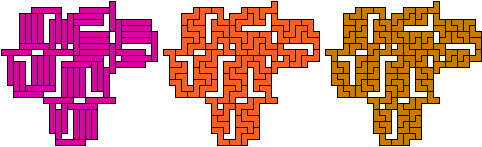
Smaller solutions have since been found; see the table below.
Table of Results
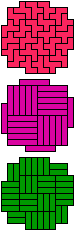
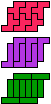
| 5F-5I-3I | 5F-5I-3L | 5F-5L-3I | 5F-5L-3L | 5F-5N-3I | 5F-5N-3L |
|---|---|---|---|---|---|
| 
| 
| 
| 
| 
|
| 120 | 60 | 30 | 15 | 60 | 30 |
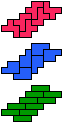
| 5F-5P-3I | 5F-5P-3L | 5F-5T-3I | 5F-5T-3L | 5F-5U-3I | 5F-5U-3L |
| 
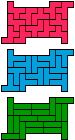
| 
| 
| 
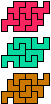
| 
|
| 30 | 15 | 60 | 30 | 60 | 30 |
| 5F-5V-3I | 5F-5V-3L | 5F-5W-3I | 5F-5W-3L | 5F-5X-3I | 5F-5X-3L |
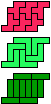
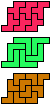
| 
| 
| 
| 
| 
|
| 30 | 30 | 30 | 30 | 30 | |
| 5F-5Y-3I | 5F-5Y-3L | 5F-5Z-3I | 5F-5Z-3L | 5I-5L-3I | 5I-5L-3L |
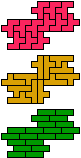
| 
| 
| 
| 
| 
|
| 60 | 15 | 60 | 30 | 30 | 30 |
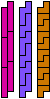
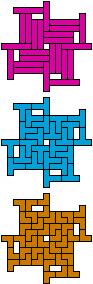
| 5I-5N-3I | 5I-5N-3L | 5I-5P-3I | 5I-5P-3L | 5I-5T-3I | 5I-5T-3L |
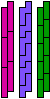
| 
| 
| 
| 
| 
|
| 30 | 30 | 30 | 30 | 30 | |
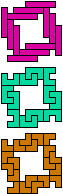
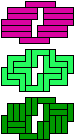
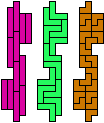
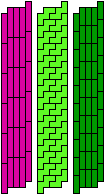
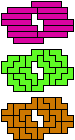
| 5I-5U-3I | 5I-5U-3L | 5I-5V-3I | 5I-5V-3L | 5I-5W-3I | 5I-5W-3L |

| 
| 
| 
| 
| 
|
| 60 | 60 | 60 | 60 | 150 | 60 |
| 5I-5X-3I | 5I-5X-3L | 5I-5Y-3I | 5I-5Y-3L | 5I-5Z-3I | 5I-5Z-3L |

| 
| 
| 
| 
| 
|
| 30 | 30 | 150 | |||
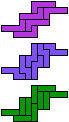
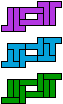
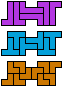
| 5L-5N-3I | 5L-5N-3L | 5L-5P-3I | 5L-5P-3L | 5L-5T-3I | 5L-5T-3L |
| 
| 
| 
| 
| 
|
| 30 | 30 | 15 | 15 | 30 | 30 |
| 5L-5U-3I | 5L-5U-3L | 5L-5V-3I | 5L-5V-3L | 5L-5W-3I | 5L-5W-3L |

| 
| 
| 
| 
| 
|
| 30 | 30 | 30 | 30 | 30 | 30 |
| 5L-5X-3I | 5L-5X-3L | 5L-5Y-3I | 5L-5Y-3L | 5L-5Z-3I | 5L-5Z-3L |

| 
| 
| 
| 
| 
|
| 240 | 30 | 30 | 60 | 30 | |
| 5N-5P-3I | 5N-5P-3L | 5N-5T-3I | 5N-5T-3L | 5N-5U-3I | 5N-5U-3L |
| 
| 
| 
| 
| 
|
| 30 | 15 | 30 | 30 | 30 | 30 |
| 5N-5V-3I | 5N-5V-3L | 5N-5W-3I | 5N-5W-3L | 5N-5X-3I | 5N-5X-3L |

| 
| 
| 
| 
| 
|
| 30 | 30 | 30 | 30 | 120 | |
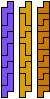
| 5N-5Y-3I | 5N-5Y-3L | 5N-5Z-3I | 5N-5Z-3L | 5P-5T-3I | 5P-5T-3L |
| 
| 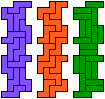
| 
| 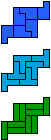
| 
|
| 30 | 30 | 60 | 30 | 30 | 30 |
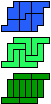
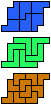
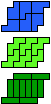
| 5P-5U-3I | 5P-5U-3L | 5P-5V-3I | 5P-5V-3L | 5P-5W-3I | 5P-5W-3L |

| 
| 
| 
| 
| 
|
| 30 | 30 | 30 | 30 | 30 | 15 |
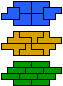
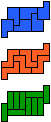
| 5P-5X-3I | 5P-5X-3L | 5P-5Y-3I | 5P-5Y-3L | 5P-5Z-3I | 5P-5Z-3L |

| 
| 
| 
| 
| 
|
| 30 | 30 | 30 | 30 | 30 | |
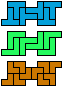
| 5T-5U-3I | 5T-5U-3L | 5T-5V-3I | 5T-5V-3L | 5T-5W-3I | 5T-5W-3L |

| 
| 
| 
| 
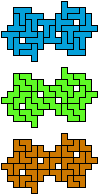
| 
|
| 30 | 60 | 60 | 30 | 120 | 90 |
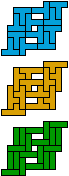
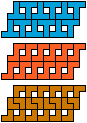
| 5T-5X-3I | 5T-5X-3L | 5T-5Y-3I | 5T-5Y-3L | 5T-5Z-3I | 5T-5Z-3L |

| 
| 
| 
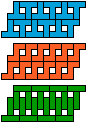
| 
| 
|
| 30 | 60 | 30 | 60 | 60 | |
| 5U-5V-3I | 5U-5V-3L | 5U-5W-3I | 5U-5W-3L | 5U-5X-3I | 5U-5X-3L |

| 
| 
| 
| 
| 
|
| 30 | 30 | 30 | 30 | ||
| 5U-5Y-3I | 5U-5Y-3L | 5U-5Z-3I | 5U-5Z-3L | 5V-5W-3I | 5V-5W-3L |
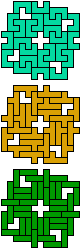
| 
| 
| 
| 
| 
|
| 120 | 30 | 60 | 60 | 30 | 30 |
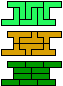
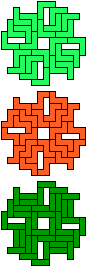
| 5V-5X-3I | 5V-5X-3L | 5V-5Y-3I | 5V-5Y-3L | 5V-5Z-3I | 5V-5Z-3L |

| 
| 
| 
| 
| 
|
| 30 | 60 | 120 | 30 | ||
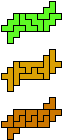
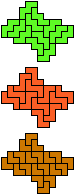
| 5W-5X-3I | 5W-5X-3L | 5W-5Y-3I | 5W-5Y-3L | 5W-5Z-3I | 5W-5Z-3L |

| 
| 
| 
| 
| 
|
| 60 | 30 | 60 | |||
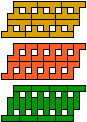
| 5X-5Y-3I | 5X-5Y-3L | 5X-5Z-3I | 5X-5Z-3L | 5Y-5Z-3I | 5Y-5Z-3L |

| 
| 
| 
| 
| 
|
| 30 | 60 | 30 |
Last revised 2019-08-22.
Back to Multiple Compatibility < Polyform Compatibility < Polyform Curiosities
Col. George Sicherman [ HOME | MAIL ]