Holeless Triple Pentominoes

Introduction

Livio Zucca's Triple Pentominoes studies the problem of finding a compatibility figure for three pentominoes. Here I show holeless variants for triple pentominoes. The green cells represent holeless solutions that already appear on Triple Pentominoes.

Only closed solutions are shown. For reëntrant solutions see Triple Pentominoes.

Summary

F I L10 F I N10 F I P10 F I T? F I U? F I V30 F I W10 F I X× F I Y10 F I Z?
F L N4 F L P4 F L T2 F L U? F L V6 F L W2 F L X× F L Y4 F L Z4 F N P4
F N T12 F N U8 F N V8 F N W6 F N X16 F N Y8 F N Z2 F P T4 F P U8 F P V6
F P W4 F P X4 F P Y2 F P Z2 F T U? F T V8 F T W16 F T X4 F T Y4 F T Z?
F U V? F U W4 F U X× F U Y? F U Z? F V W6 F V X× F V Y8 F V Z? F W X×
F W Y2 F W Z10 F X Y2 F X Z× F Y Z2 I L N4 I L P2 I L T32 I L U? I L V28
I L W10 I L X× I L Y4 I L Z? I N P2 I N T? I N U? I N V60 I N W10 I N X×
I N Y2 I N Z? I P T32 I P U? I P V10 I P W10 I P X× I P Y2 I P Z? I T U?
I T V? I T W? I T X× I T Y? I T Z? I U V? I U W? I U X× I U Y? I U Z?
I V W30 I V X× I V Y50 I V Z? I W X× I W Y24 I W Z? I X Y× I X Z× I Y Z?
L N P4 L N T8 L N U8 L N V6 L N W8 L N X× L N Y4 L N Z4 L P T2 L P U6
L P V2 L P W4 L P X× L P Y4 L P Z4 L T U? L T V2 L T W? L T X× L T Y4
L T Z? L U V? L U W6 L U X× L U Y14 L U Z? L V W6 L V X× L V Y2 L V Z16
L W X× L W Y8 L W Z44 L X Y× L X Z× L Y Z4 N P T12 N P U2 N P V8 N P W2
N P X16 N P Y2 N P Z8 N T U? N T V24 N T W? N T X16 N T Y16 N T Z? N U V?
N U W2 N U X× N U Y? N U Z? N V W16 N V X× N V Y12 N V Z? N W X× N W Y8
N W Z44 N X Y16 N X Z× N Y Z8 P T U? P T V2 P T W64 P T X4 P T Y4 P T Z?
P U V? P U W2 P U X× P U Y14 P U Z? P V W6 P V X× P V Y8 P V Z4 P W X×
P W Y8 P W Z10 P X Y4 P X Z× P Y Z2 T U V? T U W? T U X× T U Y? T U Z?
T V W? T V X× T V Y4 T V Z? T W X× T W Y? T W Z? T X Y4 T X Z× T Y Z?
U V W? U V X× U V Y? U V Z? U W X× U W Y? U W Z? U X Y× U X Z× U Y Z?
V W X× V W Y72 V W Z? V X Y× V X Z× V Y Z? W X Y× W X Z× W Y Z18 X Y Z×

Solutions

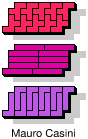
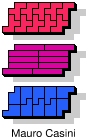
5F+5I+5L5F+5I+5N5F+5I+5P5F+5I+5T5F+5I+5U
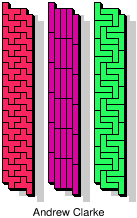
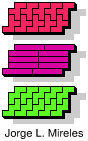
5F+5I+5V5F+5I+5W5F+5I+5X5F+5I+5Y5F+5I+5Z
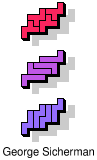
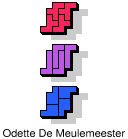
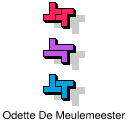
5F+5L+5N5F+5L+5P5F+5L+5T5F+5L+5U5F+5L+5V
5F+5L+5W5F+5L+5X5F+5L+5Y5F+5L+5Z5F+5N+5P
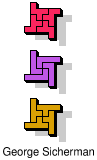
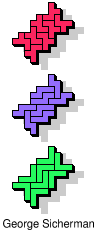
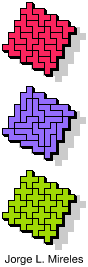
5F+5N+5T5F+5N+5U5F+5N+5V5F+5N+5W5F+5N+5X
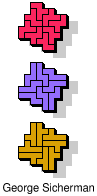
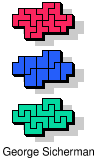
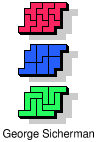
5F+5N+5Y5F+5N+5Z5F+5P+5T5F+5P+5U5F+5P+5V
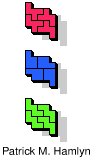
5F+5P+5W5F+5P+5X5F+5P+5Y5F+5P+5Z5F+5T+5U
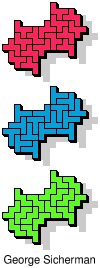
5F+5T+5V5F+5T+5W5F+5T+5X5F+5T+5Y5F+5T+5Z
5F+5U+5V5F+5U+5W5F+5U+5X5F+5U+5Y5F+5U+5Z
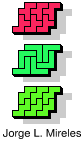
5F+5V+5W5F+5V+5X5F+5V+5Y5F+5V+5Z5F+5W+5X
5F+5W+5Y5F+5W+5Z5F+5X+5Y5F+5X+5Z5F+5Y+5Z
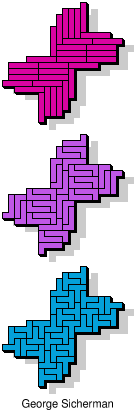
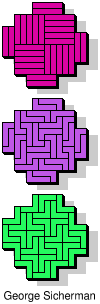
5I+5L+5N5I+5L+5P5I+5L+5T5I+5L+5U5I+5L+5V
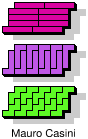
5I+5L+5W5I+5L+5X5I+5L+5Y5I+5L+5Z5I+5N+5P
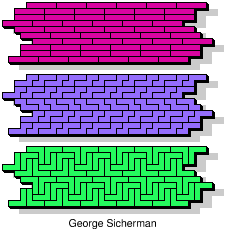
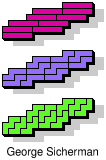
5I+5N+5T5I+5N+5U5I+5N+5V5I+5N+5W5I+5N+5X
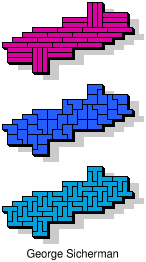
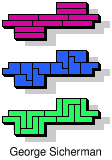
5I+5N+5Y5I+5N+5Z5I+5P+5T5I+5P+5U5I+5P+5V
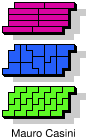
5I+5P+5W5I+5P+5X5I+5P+5Y5I+5P+5Z5I+5T+5U
5I+5T+5V5I+5T+5W5I+5T+5X5I+5T+5Y5I+5T+5Z
5I+5U+5V5I+5U+5W5I+5U+5X5I+5U+5Y5I+5U+5Z
5I+5V+5W5I+5V+5X5I+5V+5Y5I+5V+5Z5I+5W+5X
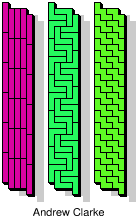
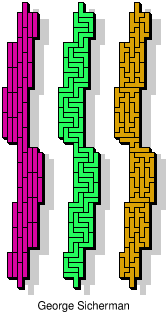
5I+5W+5Y5I+5W+5Z5I+5X+5Y5I+5X+5Z5I+5Y+5Z
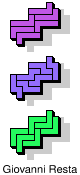
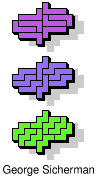
5L+5N+5P5L+5N+5T5L+5N+5U5L+5N+5V5L+5N+5W
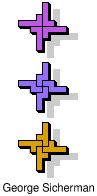
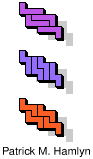
5L+5N+5X5L+5N+5Y5L+5N+5Z5L+5P+5T5L+5P+5U
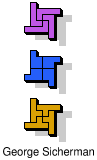
5L+5P+5V5L+5P+5W5L+5P+5X5L+5P+5Y5L+5P+5Z
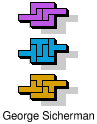
5L+5T+5U5L+5T+5V5L+5T+5W5L+5T+5X5L+5T+5Y
5L+5T+5Z5L+5U+5V5L+5U+5W5L+5U+5X5L+5U+5Y
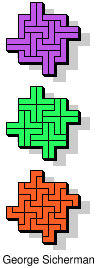
5L+5U+5Z5L+5V+5W5L+5V+5X5L+5V+5Y5L+5V+5Z
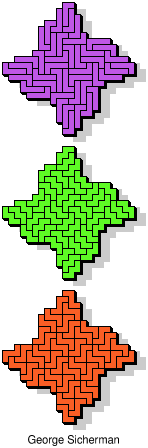
5L+5W+5X5L+5W+5Y5L+5W+5Z5L+5X+5Y5L+5X+5Z
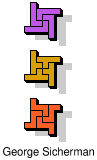
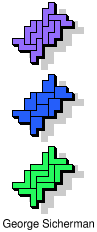
5L+5Y+5Z5N+5P+5T5N+5P+5U5N+5P+5V5N+5P+5W
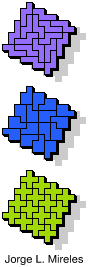
5N+5P+5X5N+5P+5Y5N+5P+5Z5N+5T+5U5N+5T+5V
5N+5T+5W5N+5T+5X5N+5T+5Y5N+5T+5Z5N+5U+5V
5N+5U+5W5N+5U+5X5N+5U+5Y5N+5U+5Z5N+5V+5W
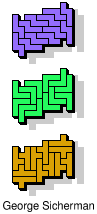
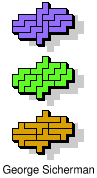
5N+5V+5X5N+5V+5Y5N+5V+5Z5N+5W+5X5N+5W+5Y
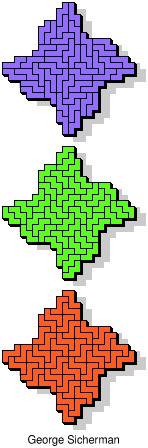
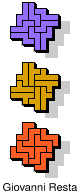
5N+5W+5Z5N+5X+5Y5N+5X+5Z5N+5Y+5Z5P+5T+5U
5P+5T+5V5P+5T+5W5P+5T+5X5P+5T+5Y5P+5T+5Z
5P+5U+5V5P+5U+5W5P+5U+5X5P+5U+5Y5P+5U+5Z
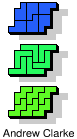
5P+5V+5W5P+5V+5X5P+5V+5Y5P+5V+5Z5P+5W+5X
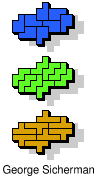
5P+5W+5Y5P+5W+5Z5P+5X+5Y5P+5X+5Z5P+5Y+5Z
5T+5U+5V5T+5U+5W5T+5U+5X5T+5U+5Y5T+5U+5Z
5T+5V+5W5T+5V+5X5T+5V+5Y5T+5V+5Z5T+5W+5X
5T+5W+5Y5T+5W+5Z5T+5X+5Y5T+5X+5Z5T+5Y+5Z
5U+5V+5W5U+5V+5X5U+5V+5Y5U+5V+5Z5U+5W+5X
5U+5W+5Y5U+5W+5Z5U+5X+5Y5U+5X+5Z5U+5Y+5Z
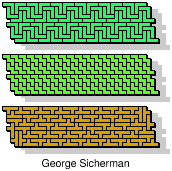
5V+5W+5X5V+5W+5Y5V+5W+5Z5V+5X+5Y5V+5X+5Z
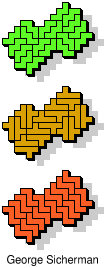
5V+5Y+5Z5W+5X+5Y5W+5X+5Z5W+5Y+5Z5X+5Y+5Z

Last revised 2014-10-17.

Back to Multiple Compatibility.
Back to Polyform Compatibility.
Back to Polyform Curiosities.
George Sicherman [ HOME | MAIL ]