Baiocchi Figures for Hexomino Pairs
A Baiocchi figure is a figure
formed by joining copies of a polyform and having the maximal
symmetry for the polyform's class.
For polyominoes, that means square symmetry, or 4-way rotary with reflection.
If a polyomino lacks diagonal symmetry, its Baiocchi figures
must be Galvagni figures or contain Galvagni figures.
Claudio
Baiocchi proposed the idea in January 2008.
Baiocchi figures first appeared in Erich Friedman's
Math Magic for that month.
We can also define Baiocchi Figures for sets of polyominoes.
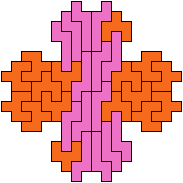
Here I show minimal known Baiocchi Figures for pairs of hexominoes.
The figures must use at least one copy of each hexomino.
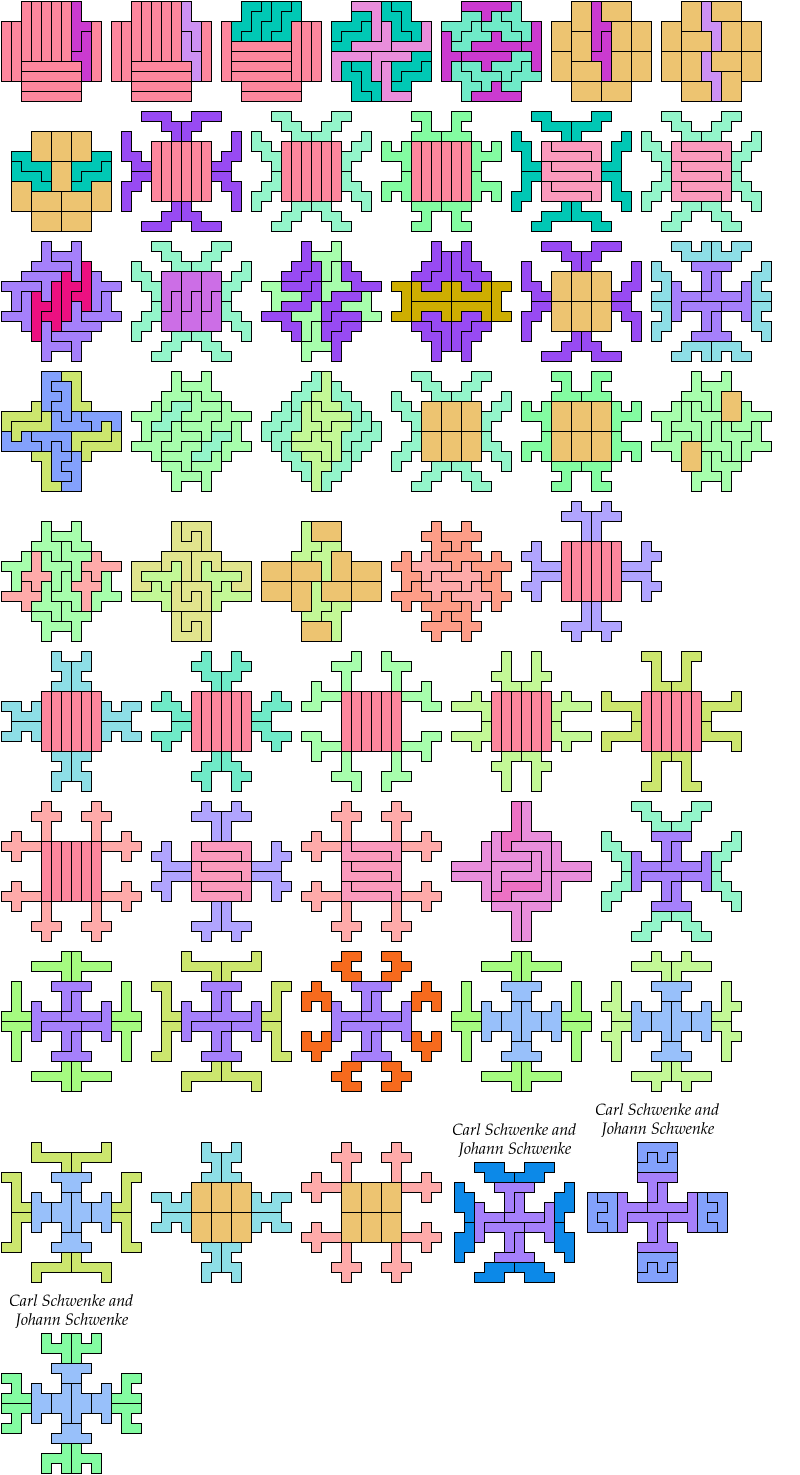
Carl Schwenke and Johann Schwenke solved one holeless case
and improved many other holeless solutions.
See also Baiocchi Figures
for Pentomino Pairs.
4 Tiles

6 Tiles

8 Tiles

10 Tiles
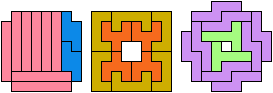
12 Tiles
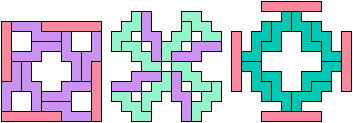 Holeless solutions shown above are not reproduced here.
Holeless solutions shown above are not reproduced here.
6 Tiles

8 Tiles
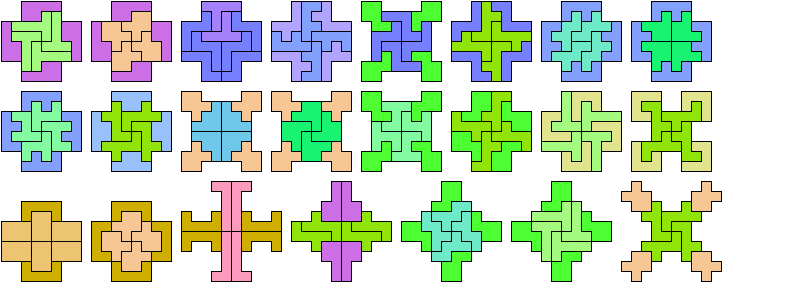
10 Tiles

12 Tiles

14 Tiles
16 Tiles

18 Tiles
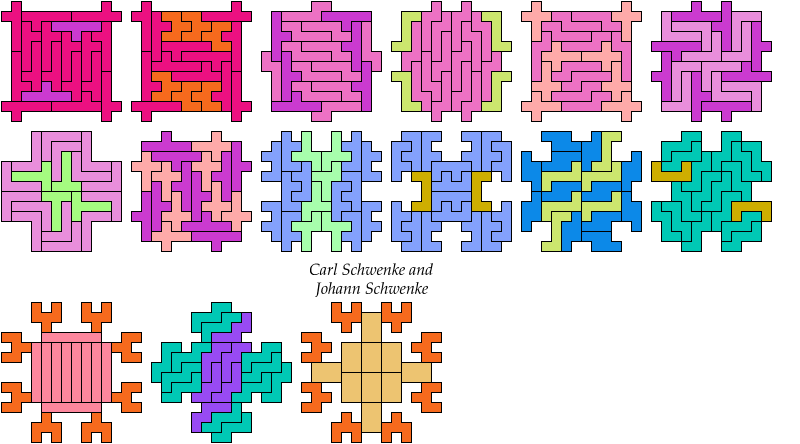
20 Tiles

22 Tiles

24 Tiles
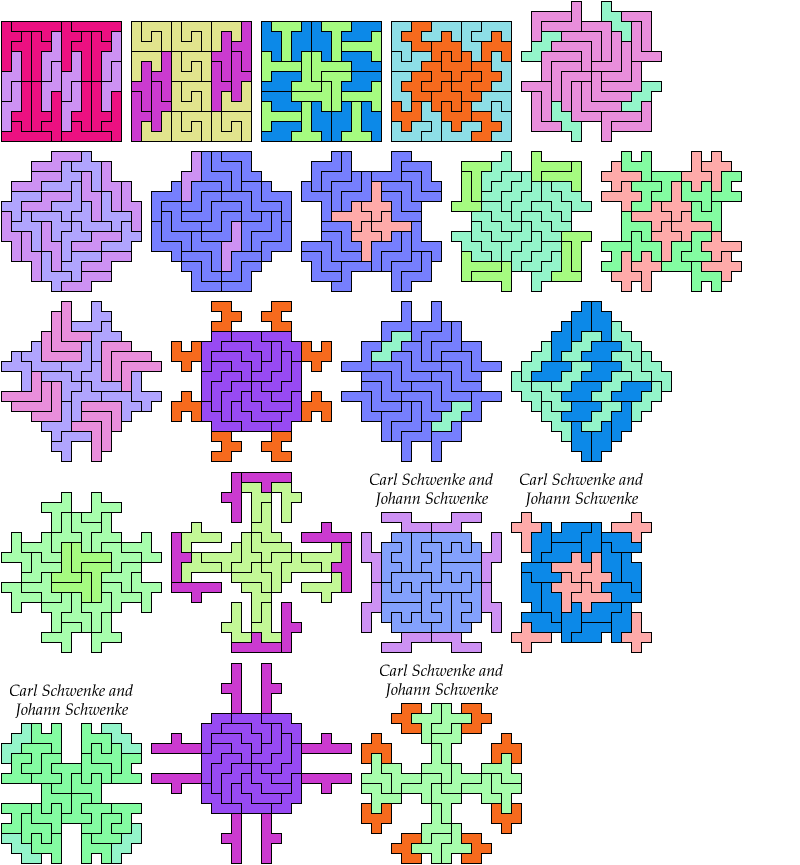
26 Tiles
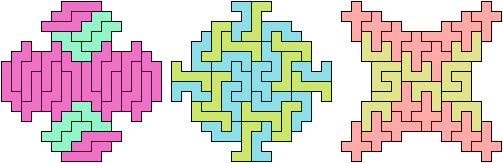
28 Tiles
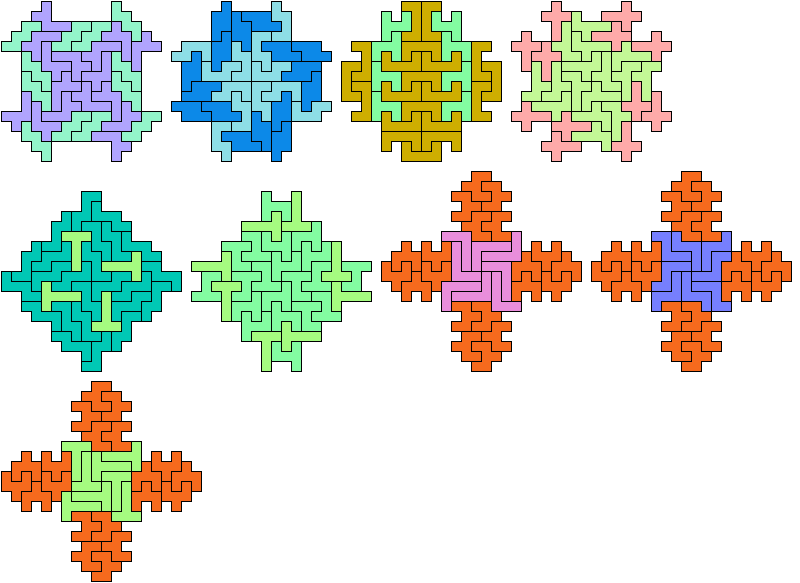
30 Tiles
32 Tiles
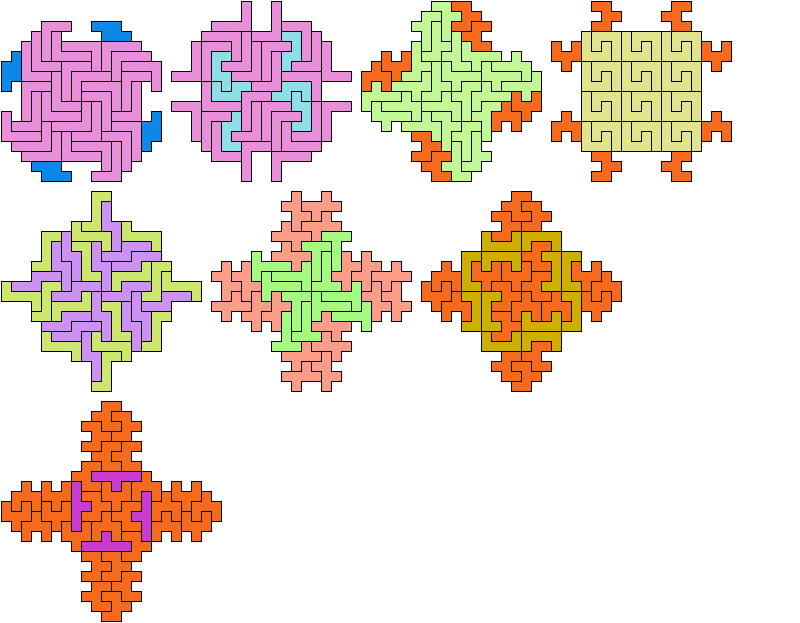
36 Tiles
40 Tiles
48 Tiles
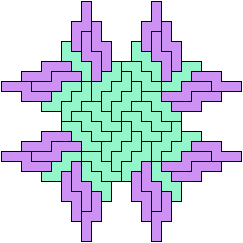
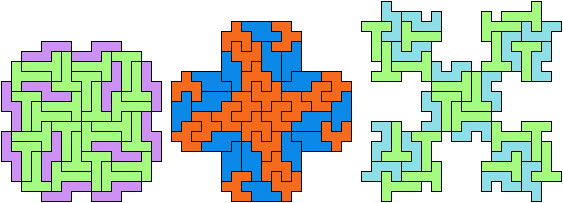
52 Tiles

54 Tiles
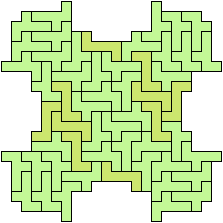
64 Tiles
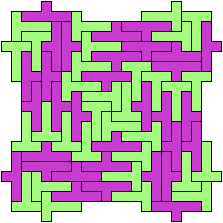
Unsolved Holeless
Last revised 2024-04-18.
Back to Baiocchi Figures
<
Polyform Compatibility
<
Polyform Curiosities
George Sicherman
[ HOME
| MAIL
]

























