Galvagni Figures & Reid Figures for Octominoes
A octomino is a figure made of eight squares joined
edge to edge.
A Galvagni figure is a figure that can be tiled by a polyform
in more than one way—a kind of self-compatibility figure.
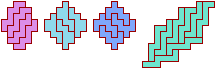
A Reid figure is a Galvagni figure without holes.
Some of these figures were found by
Michael
Reid of the University of Central Florida.
For pentominoes, see Galvagni Figures & Reid Figures
for Pentominoes.
For hexominoes, see Galvagni Figures & Reid Figures
for Hexominoes.
For heptominoes, see Galvagni Figures & Reid Figures
for Heptominoes.
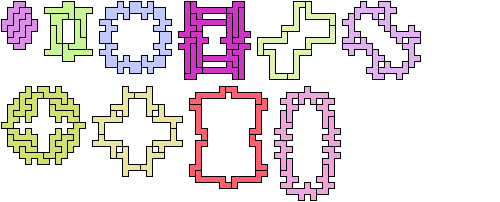
Here are minimal known Galvagni figures and Reid figures for octominoes.
Galvagni Figures
2 Tiles

3 Tiles

4 Tiles

6 Tiles

8 Tiles

10 Tiles
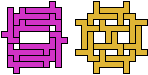
12 Tiles
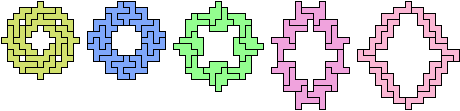
16 Tiles
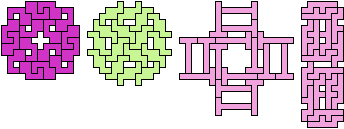
20 Tiles
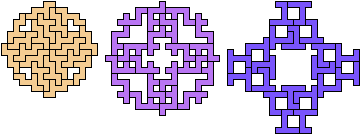
28 Tiles
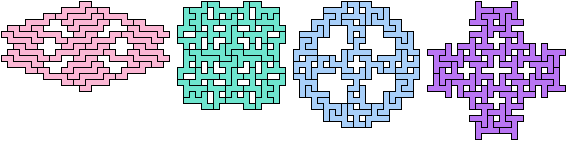
40 Tiles
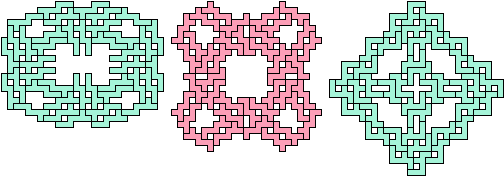
52 Tiles

64 Tiles
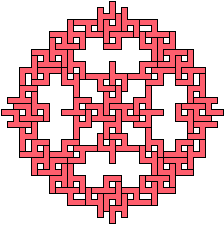
72 Tiles
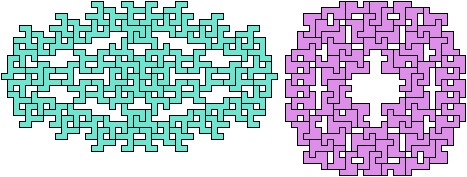
Unsolved

Impossible

Hypersymmetric Variants
Reid Figures

Hypersymmetric Variants
Last revised 2015-04-27.
Back to Galvagni Compatibility
<
Polyform Compatibility
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]


















