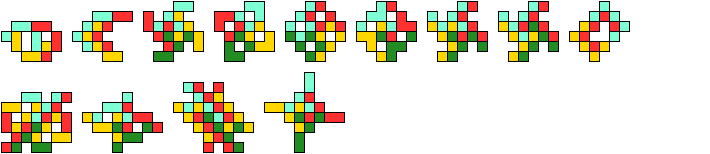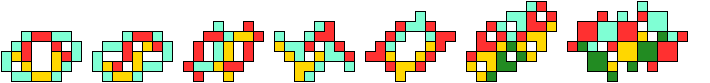Polyking Integration

Introduction

A polyking is a set of squares in the square grid, joined edge to edge or corner to corner. It differs from a polyomino, whose cells must be joined edge to edge. For example, there is only one monoking, the monomino. There are two dikings:

To integrate a polyking is to arrange copies of it without overlapping to form a polyomino. Here I show minimal known integrations of polykings. The solutions shown are not necessarily uniquely minimal.

Not every polyking can be integrated. The smallest that cannot are octakings. Here are some examples:

Where several solutions for a polyking have the same number of tiles, I prefer one whose tiles do not cross.

  • Monoking
  • Dikings
  • Trikings
  • Tetrakings
  • Pentakings
  • Hexakings

    • Monoking

    Dikings

    Trikings

    Tetrakings

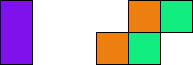
    Crossless variant

    Impossible

    Pentakings

    At most 2 tiles are needed to integrate any pentaking.

    Crossless variants

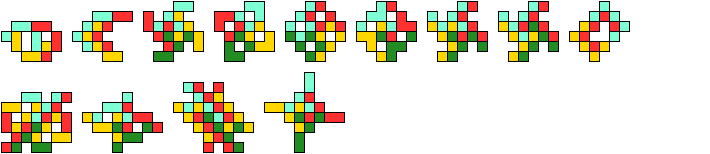
    Impossible

    Hexakings

    There are 524 hexakings, too many to show here. Instead I show only hexakings of which 3 or more copies are needed.

    3 Tiles

    4 Tiles

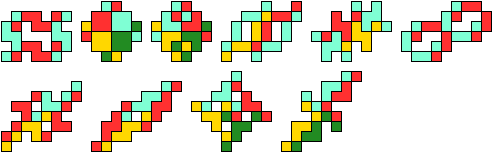
    6 Tiles

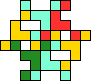
    Crossless variants

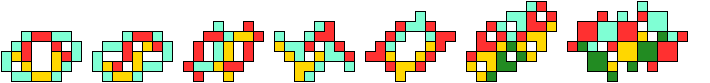
    Last revised 2024-05-14.

    Back to Polyform Exclusion, Equalization, Variegation, and Integration < Polyform Curiosities
    Col. George Sicherman [ HOME | MAIL ]