Two-sided polynars may be rotated and reflected. One-sided polynars may be rotated but not reflected.
Polynars were first studied by László Molnár. Previously, around 2004, Saturo Natsuki (夏木智) invented some puzzles using pieces made with three cubes—three-dimensional trinars.
| Order | Two-Sided A390620 | One-Sided A390621 |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 2 | 3 |
| 3 | 9 | 13 |
| 4 | 60 | 112 |
| 5 | 467 | 896 |
| 6 | 4 226 | 8 381 |
| 7 | 39 972 | 79 614 |
| 8 | 390 903 | 781 140 |
| 9 | 3 886 181 | 7 769 317 |
| 10 | 39 154 600 | 78 302 759 |
| 11 | 398 364 048 | 796 698 959 |
The figures below show two-sided polynars.

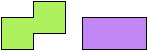
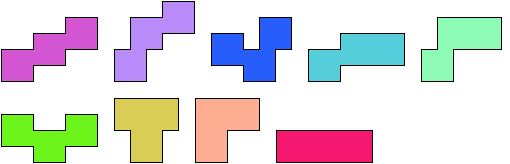

Last revised 2026-01-27.