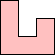Cell Shifts for Polyominoes
Introduction
Two figures can be tiled with copies of the same
polyomino.
The figures differ in only one cell.
How near can the unmatched cells lie?
Over all such pairs of figures,
a minimal vector from one unmatched cell to the other
is called a minimal shift vector.
Here I show minimal shift vectors
for polyominoes up to order 5.
Values in red are unproven.
The nontrivial proven values are by Mike Reid,
using
Tile Homotopy Theory.
If you can solve any of the unsolved cases,
please let me know.
For heptominoes, see Cell Shifts for Heptominoes.
Monomino
 | (1, 0) |  |
Domino
 | (1, 1) |  |
Trominoes
Tetrominoes
 | (4, 0) |  |
 | (2, 0) |  |
 | (1, 1) |  |
 | (2, 2) |  |
 | — | |
Pentominoes
 | (5, 0) |  |
 | (1, 0) | 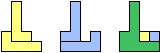 |
 | (1, 0) |  |
 | (1, 0) |  |
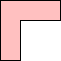 | (6, 0)
|  Mike Reid Mike Reid |
 | (1, 0) |  |
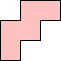 | (1, 0) |  |
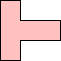 | (3, 0) | 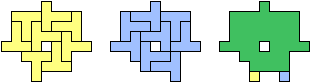 |
 | (1, 0) |  |
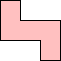 | (5, 0) |  |

| (1, 0) |  Mike Reid Mike Reid |
 | — | |
Symmetric Variants
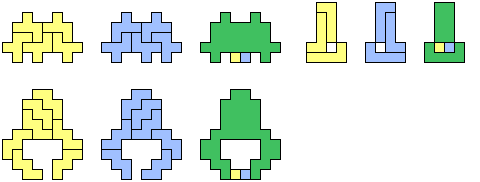
Hexominoes
 | (6, 0) |  |
 | (1, 1) | 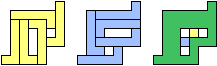 |
 | (2, 0) | 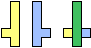 |
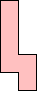
| (3, 3) | 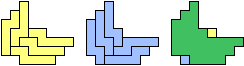 Mike Reid Mike Reid |
 | (3, 3) |  |
 | (2, 0)
| 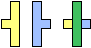 |
 | (1, 1) | 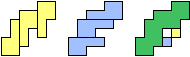 |
 | (12, 0) |  |
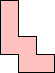 | (1, 1)
| 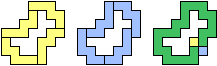 Mike Reid Mike Reid |
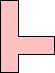 | (1, 1) |  |
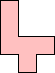 | (2, 2) |  |
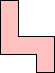 | (1, 1) |  |

| (2, 2) |  Mike Reid Mike Reid |
 | (3, 3) | 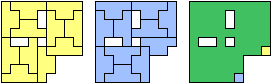 |
 | (6, 0) | 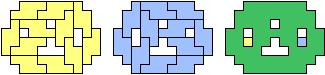 |
 | (4, 0)
|  Mike Reid Mike Reid |
 | (4, 0) |  |
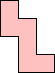 | (1, 1) |  |
 | (2, 0)
|  Mike Reid Mike Reid |
 | (3, 3) |  |
 | (1, 1)
|  Mike Reid Mike Reid |
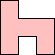 | (2, 0) |  |
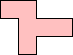 | (1, 1) |  |
 | (1, 1) |  |
 | (6, 6) | 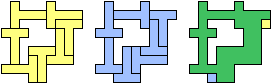 |

| (1, 1) | 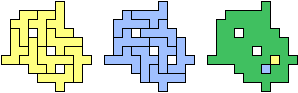 |
 | (4, 0)
|  Erich Friedman Erich Friedman |

| — | |
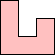 | (1, 1) |  |

| — | |
 | (3, 3) | 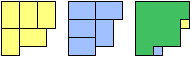 |
 | (2, 0) |  |
 | (3, 3) | 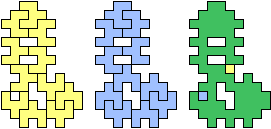 |
 | (3, 3) |  |
 | (2, 2) |  |
Monomino
 | (1, 0) |  |
Domino
 | (2, 0) |  |
Trominoes
Tetrominoes
 | (4, 0) |  |
 | (4, 0) |  |
 | (2, 0) |  |
 | (4, 4) | 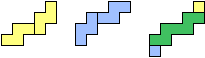 |
 | — | |
Pentominoes
 | (5, 0) |  |
 | (1, 0) |  |
 | (1, 0) | 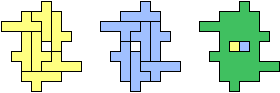 |
 | (1, 0) | 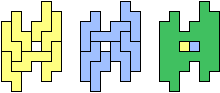 |
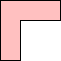 | (6, 0) |  |
 | (1, 0) | 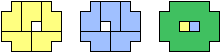 |
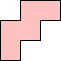 | (1, 0) | 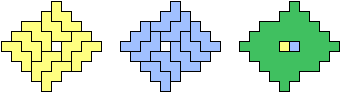 |
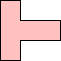 | (3, 0) | 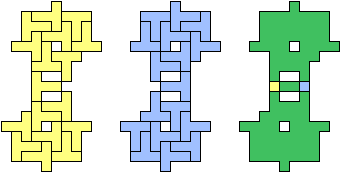 |
 | (1, 0) |  |
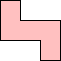 | (5, 0) |  |

| (1, 0) |  Mike Reid Mike Reid |
 | — | |
Hexominoes
 | (6, 0) |  |
 | (2, 0) |  |
 | (2, 2) |  |
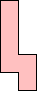 | (6, 0) |  |
 | (6, 0) | 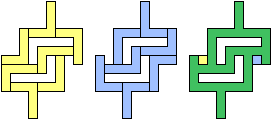 |
 | (2, 0) | 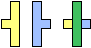 |
 | (2, 0) | 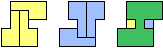 |
 | (12, 0) | 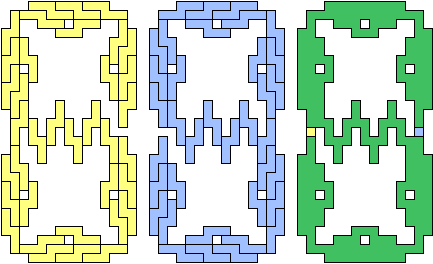 |
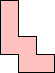 | (2, 0) | 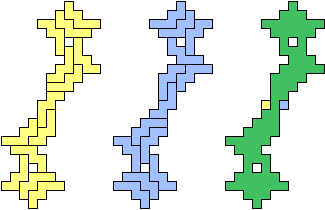 |
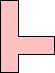 | (2, 0) | 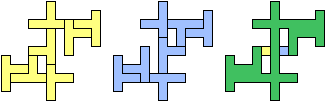 |
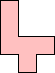 | (4, 0) | 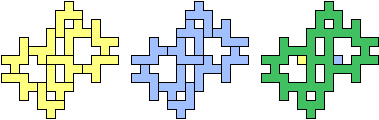 |
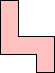 | (2, 0) | 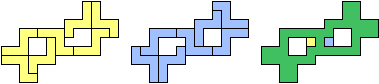 |
 | (4, 0) |  |
 | (6, 0) |  |
 | (6, 6) | 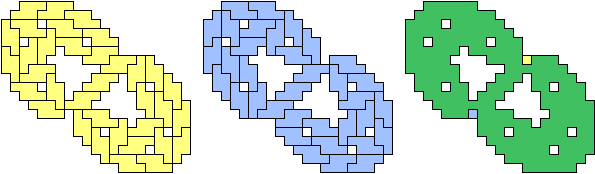 |
 | (4, 0) |  |
 | (4, 0) | 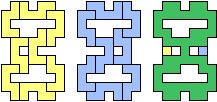 |
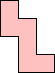 | (2, 0) |  |
 | (2, 2) |  |
 | (6, 0) | 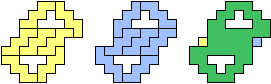 |
 | (2, 0) | 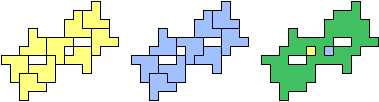 |
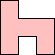 | (2, 2) |  |
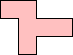 | (2, 0) | 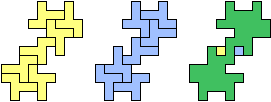 |
 | (2, 0) |  |
 | (12, 0) | 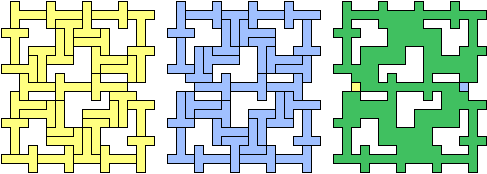 |
 | (2, 0) | 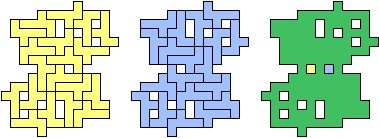 |
 | (4, 0)
|  Erich Friedman Erich Friedman |

| — | |
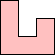 | (2, 0) | 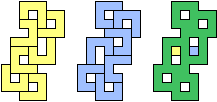 |

| — | |
 | (6, 0) | 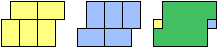 |
 | (2, 2) |  |
 | (6, 0) | 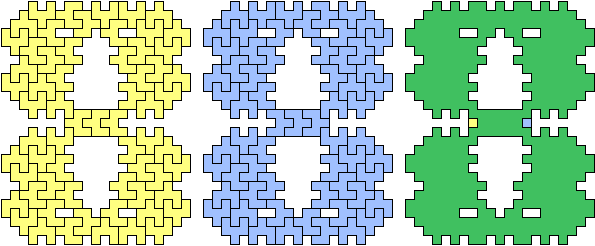 |
 | (6, 0) | 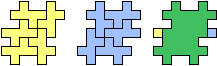 |
 | (4, 0) |  |
Last revised 2013-07-01.
Back to Polyform Cell Shifting
<
Polyform Compatibility
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]


























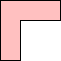
 Mike Reid
Mike Reid

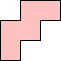

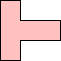



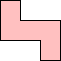


 Mike Reid
Mike Reid






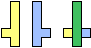
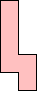
 Mike Reid
Mike Reid


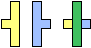




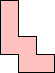
 Mike Reid
Mike Reid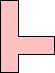

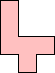

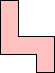


 Mike Reid
Mike Reid




 Mike Reid
Mike Reid

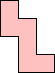


 Mike Reid
Mike Reid


 Mike Reid
Mike Reid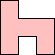

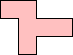








 Erich Friedman
Erich Friedman
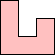


















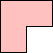


















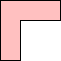



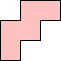

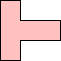



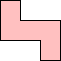


 Mike Reid
Mike Reid






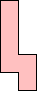




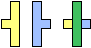




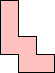

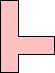

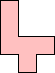

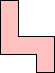











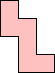







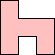

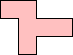








 Erich Friedman
Erich Friedman