Polyhex Tri-Oddities

A polyhex tri-oddity is a figure with ternary symmetry formed by some number of copies of a polyhex that is not a multiple of three. Torsten Sillke first studied them in 1996.

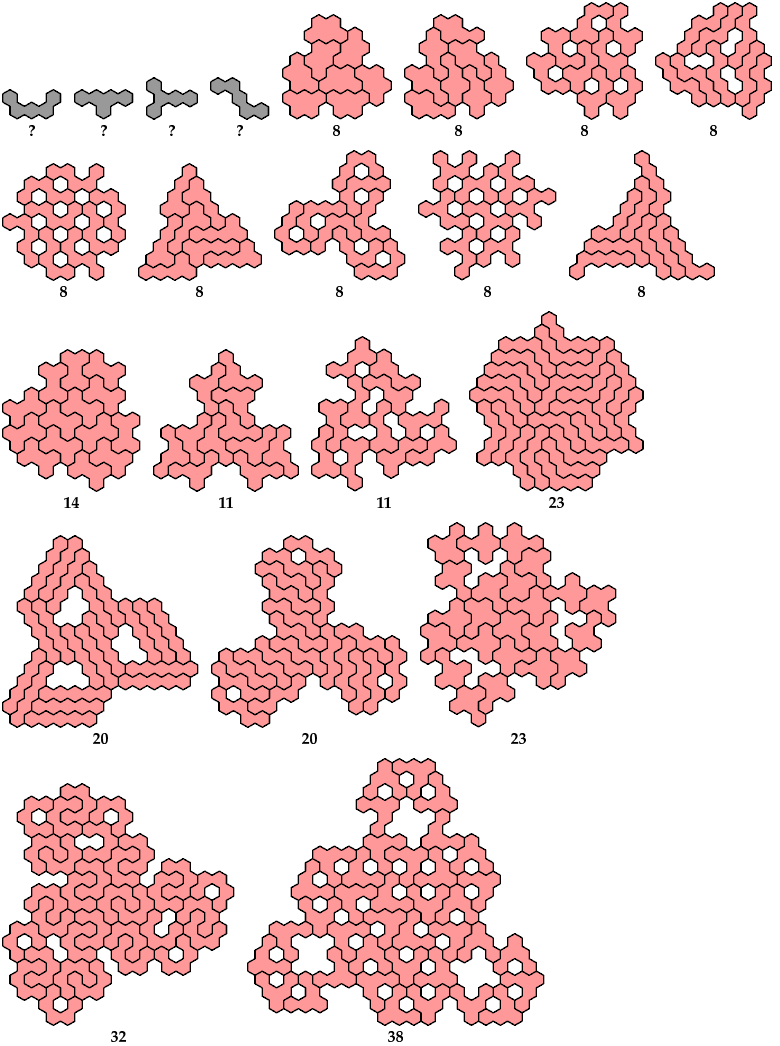
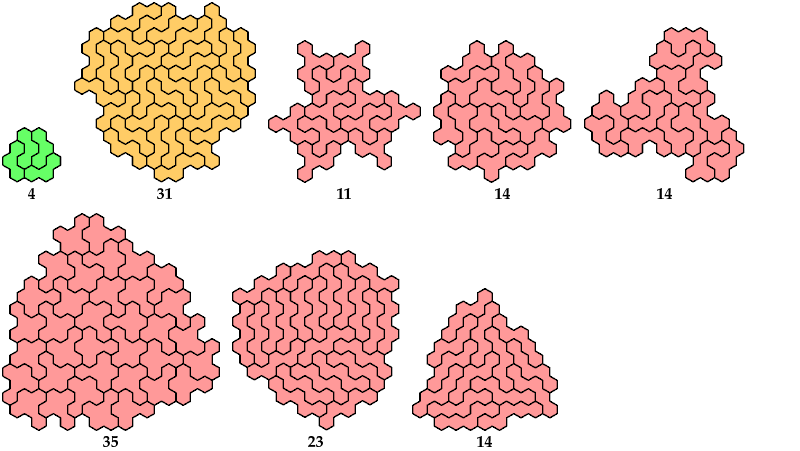
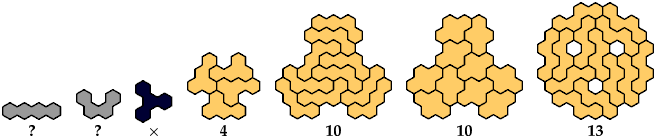
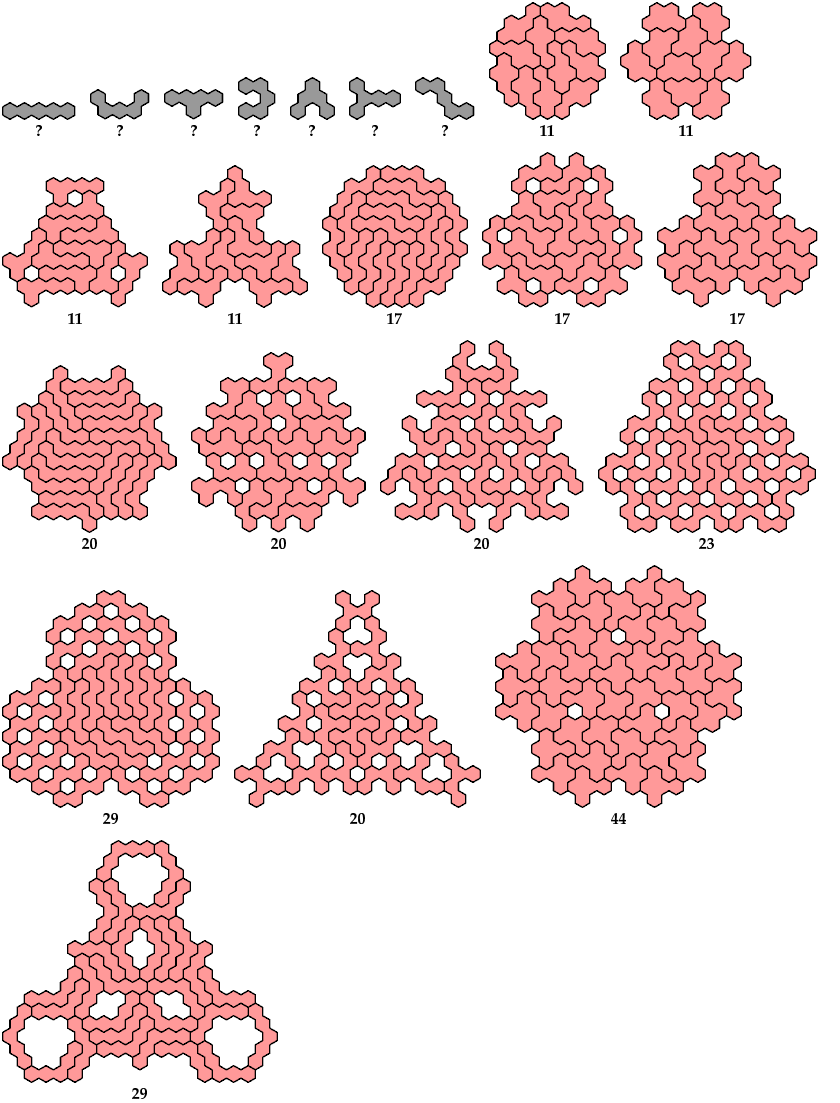
Here are the minimal known tri-oddities for the dihex, trihexes, tetrahexes, and pentahexes. Please write if you find a smaller solution or solve an unsolved case.

Mike Reid proved that the straight trihex has no solution.

For hexahexes, see Hexahex Tri-Oddities.

[ Dihex | Trihexes | Tetrahexes | Pentahexes | Mirror Symmetry ]

Dihex

Trihexes

Tetrahexes

Pentahexes

Holeless Variants

Mirror Symmetry

These figures have mirror symmetry as well as ternary symmetry.

Horizontal

Holeless Variants

Vertical

Holeless Variants

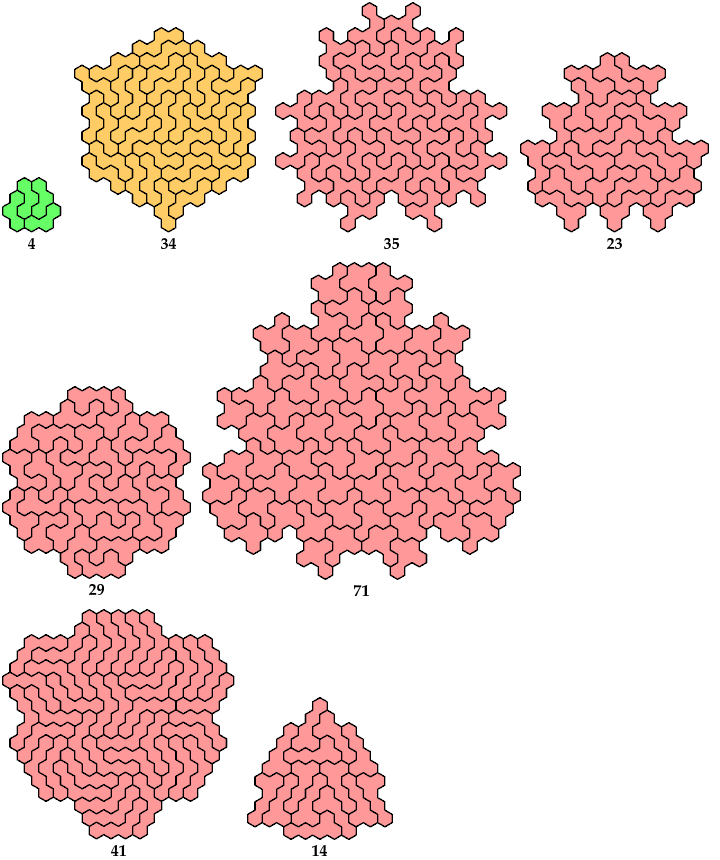
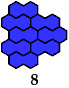
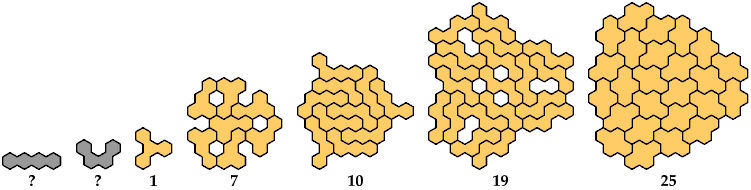
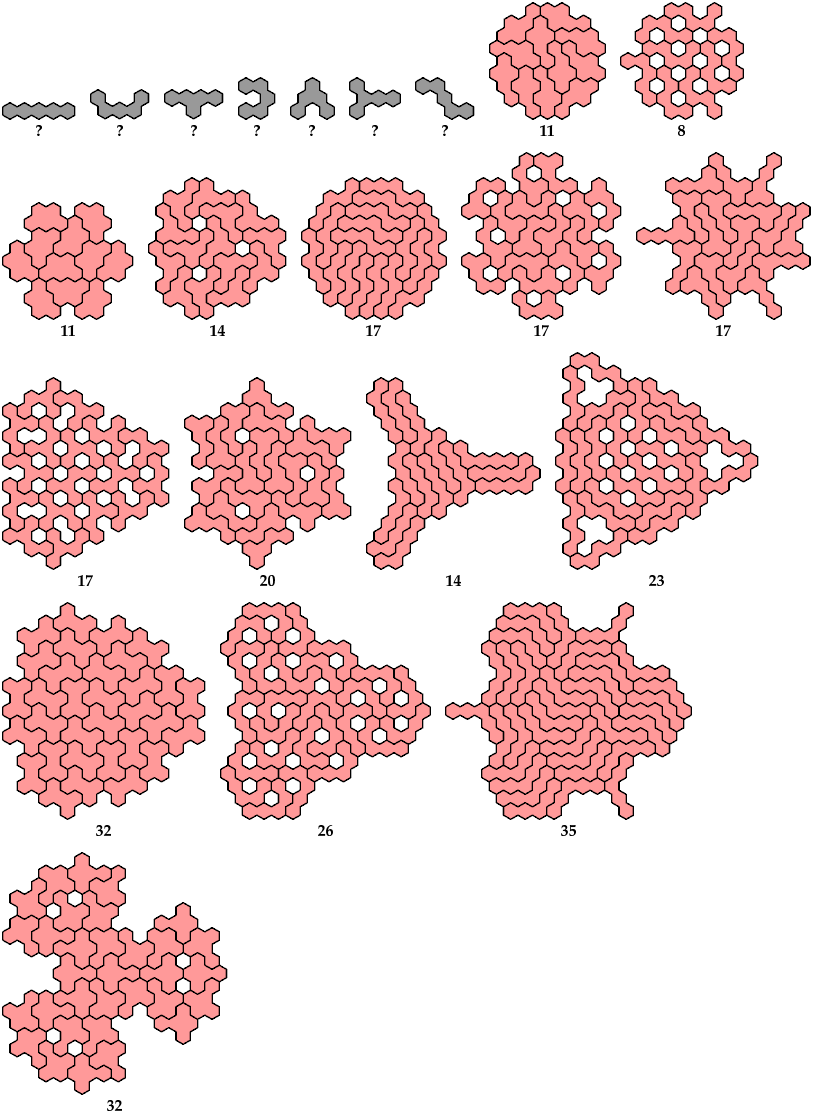
Last revised 2021-08-08.

Back to Polyform Oddities < Polyform Curiosities
Col. George Sicherman [ HOME | MAIL ]