Trihex-Pentahex Oddities
A polyhex oddity
is a symmetrical figure formed by an odd number of copies of
a polyhex.
Symmetrical figures can also be formed with copies of two
different polyhexes.
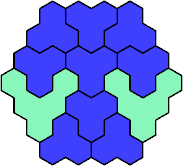
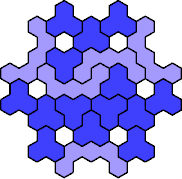
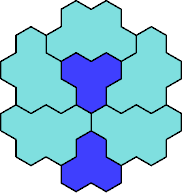
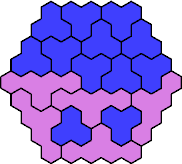
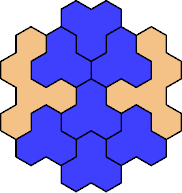
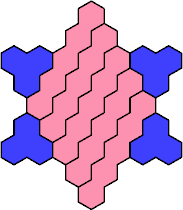
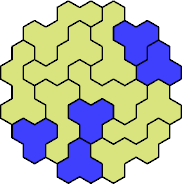
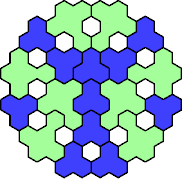
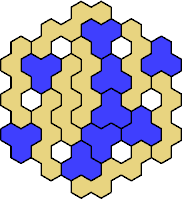
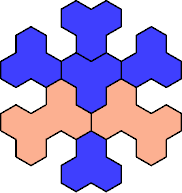
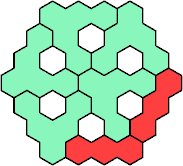
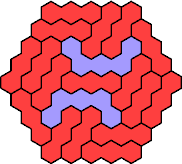
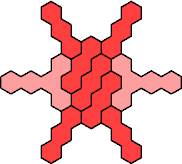
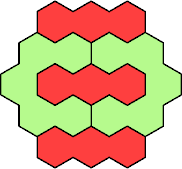
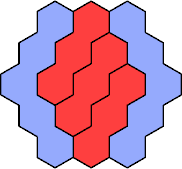
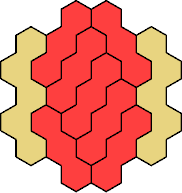
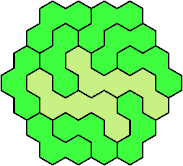
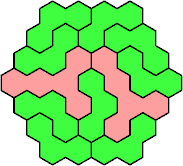
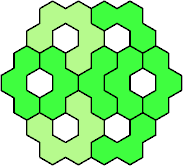
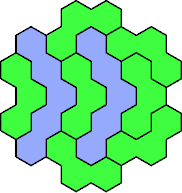
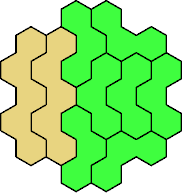
Here are the smallest known fully symmetric polyhexes with an odd
number of cells, formed by copies of a given trihex and pentahex,
using at least one of each.
The numbers show the numbers of cells.
See also
Tetrahex-Pentahex Oddities
and Pentahex Pair Oddities.
Johann Schwenke improved on one of my solutions.
| 3A+5A 37 | 3A+5C 67 | 3A+5D 31 | 3A+5E 61 | 3A+5F 31 |
|---|
| 
| 
| 
| 
|
| 3A+5H 31 | 3A+5I 37 | 3A+5J 37 | 3A+5K 55 | 3A+5L 37 |
|---|
| 
| 
| 
| 
|
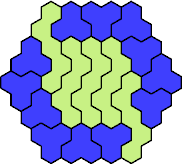
| 3A+5N 19 | 3A+5P 31 | 3A+5Q 73 | 3A+5R 55 | 3A+5S 61 |
|---|

| 
| 
| 
| 
|
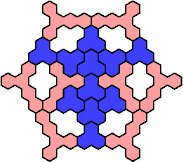
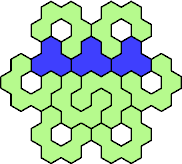
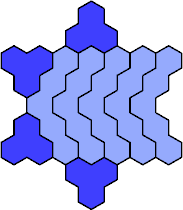
| 3A+5T 73 | 3A+5U 49 | 3A+5V 37 | 3A+5W 67 | 3A+5X 25 |
|---|
| 
| 
| 
| 
|
| 3A+5Y 25 | 3A+5Z 55 | 3I+5A 31 | 3I+5C 61 | 3I+5D 19 |
|---|

| 
| 
| 
| 
|
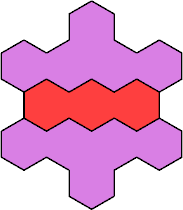
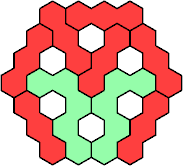
| 3I+5E 13 | 3I+5F 31 | 3I+5H 55 | 3I+5I 31 | 3I+5J 19 |
|---|
| 
| 
| 
| 
|
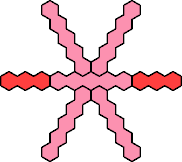
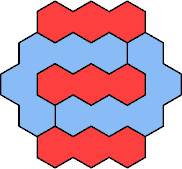
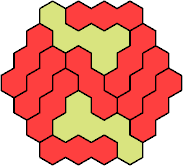
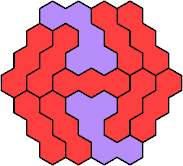
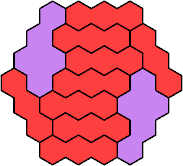
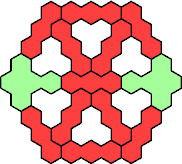
| 3I+5K 37 | 3I+5L 19 | 3I+5N 37 | 3I+5P 37 | 3I+5Q 43 |
|---|
| 
| 
| 
| 
|
| 3I+5R 37 | 3I+5S 61 | 3I+5T 31 | 3I+5U 19 | 3I+5V 19 |
|---|

| 
| 
| 
| 
|
| 3I+5W 31 | 3I+5X 49 | 3I+5Y 37 | 3I+5Z 49 | 3V+5A 31 |
|---|
| 
| 
| 
| 
|
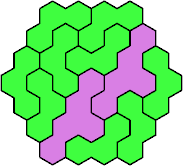
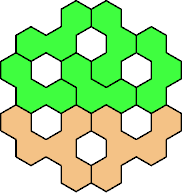
| 3V+5C 31 | 3V+5D 31 | 3V+5E 37 | 3V+5F 31 | 3V+5H 25 |
|---|

| 
| 
| 
| 
|
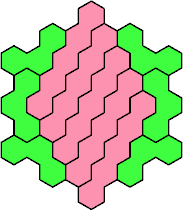
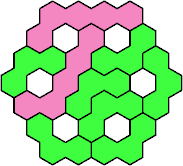
| 3V+5I 43 | 3V+5J 19 | 3V+5K 31 | 3V+5L 31 | 3V+5N 19 |
|---|
| 
| 
| 
| 
|
| 3V+5P 19 | 3V+5Q 31 | 3V+5R 31 | 3V+5S 37 | 3V+5T 37 |
|---|

| 
| 
| 
| 
|
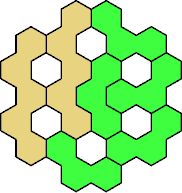
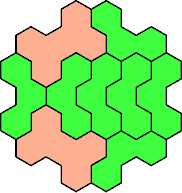
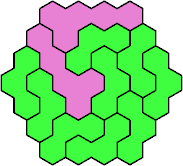
| 3V+5U 31 | 3V+5V 31 | 3V+5W 25 | 3V+5X 31 | 3V+5Y 37 |
|---|
| 
| 
| 
| 
|
| 3V+5Z 25 |
|---|
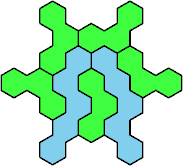
|
Solutions shown above that are holeless are not shown here.
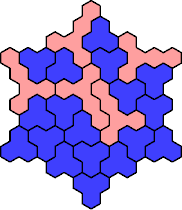
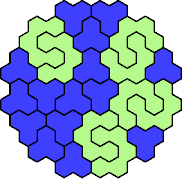
| 3A+5C — | 3A+5Q — | 3A+5T 79 | 3A+5U 85 | 3A+5W 73 |
|---|

| 
| 
| 
| 
|
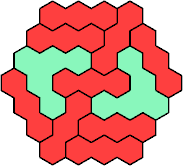
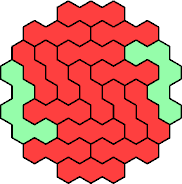
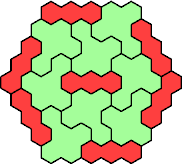
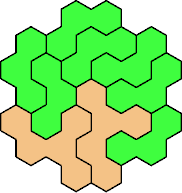
| 3I+5A 37 | 3I+5F 55 | 3I+5Q 61 | 3I+5Z 55 | 3V+5H 31 |
|---|
| 
| 
| 
| 
|
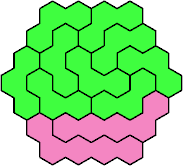
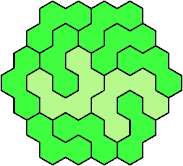
| 3V+5L 37 | 3V+5U 37 | 3V+5W 31 |
|---|
| 
| 
|
Last revised 2021-07-26.
Back to Polyform Oddities
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]













































































