| Monohex | |||||
|---|---|---|---|---|---|
 | ∞ | None | |||
| Dihex | |||||
 | 16 |  | |||
| Trihexes | |||||
 | 6 | 
|  | 10 | 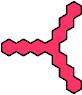 |
 | 6 |  | |||
| Tetrahexes | |||||
 | 4 | 
|  | 10 |  |
 | 6 | 
|  | 7 | 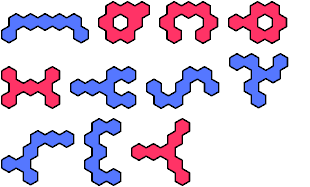 |
 | 7 | 
|  | 7 |  |
 | 4 |  | |||
| Pentahexes | |||||
 | 4 | 
|  | 6 |  |
 | 6 | 
|  | 6 | 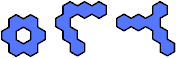 |
 | 6 | 
|  | 7 |  |
 | 6 | 
| 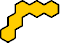 | 6 |  |
 | 7 | 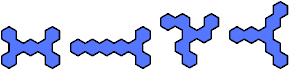
|  | 7 |  |
 | 6 | 
|  | 7 | 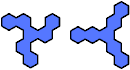 |
 | 6 | 
|  | 7 | 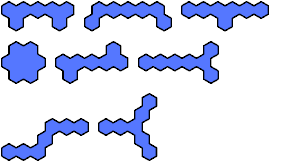 |
 | 6 | 
|  | 6 | 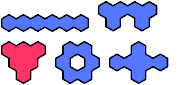 |
 | 6 | 
|  | 7 | 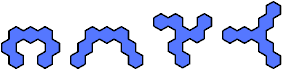 |
 | 6 | 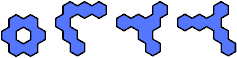
|  | 7 | 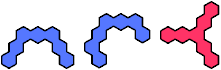 |
 | 6 | 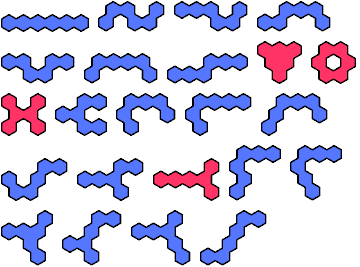
|  | 5 |  |
The compatibility problem is to find a figure that can be tiled with each of a set of polyforms. Here I show for each polyhex of orders 1 through 5 the smallest known polyhexes that are not compatible with it.
In some cases, incompatibility is probable but has not been proved by analysis or exhaustion. Proved cases are shown in red. Unproved cases are shown in blue.
Andris Cibulis first studied dihex compatibility and found the minimal polyhex incompatible with the dihex. He also found a very large compatibility for the J tetrahex.
See also Minimal Incompatibility for Polyominoes and Minimal Incompatibility for Polyiamonds.
| Monohex | |||||
|---|---|---|---|---|---|
 | ∞ | None | |||
| Dihex | |||||
 | 16 |  | |||
| Trihexes | |||||
 | 6 | 
|  | 10 |  |
 | 6 |  | |||
| Tetrahexes | |||||
 | 4 | 
|  | 10 |  |
 | 6 | 
|  | 7 |  |
 | 7 | 
|  | 7 |  |
 | 4 |  | |||
| Pentahexes | |||||
 | 4 | 
|  | 6 |  |
 | 6 | 
|  | 6 |  |
 | 6 | 
|  | 7 |  |
 | 6 | 
|  | 6 |  |
 | 7 | 
|  | 7 |  |
 | 6 | 
|  | 7 |  |
 | 6 | 
|  | 7 |  |
 | 6 | 
|  | 6 |  |
 | 6 | 
|  | 7 |  |
 | 6 | 
|  | 7 |  |
 | 6 | 
|  | 5 |  |
Last revised 2015-07-01.