Here I investigate the related question: how few cells can you remove from the plane to exclude the shape of a given polyiamond?
To exclude the diamond you must remove at least 1/2 the cells:

Here is the best known exclusion of the triamond. If you find a better one please let me know.
If triamonds are excluded, every solid cell must be adjacent to at least two holes, giving it 2/3 share in holes. So a lower bound for the hole ratio is (2/3 /[1 + 2/3]), or 2/5. There is a pattern with hole ratio 2/5 that excludes the triamond, but it is not planar! It covers the surface of a regular icosahedron:
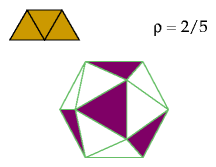
This pattern optimally excludes two tetriamonds and two pentiamonds:
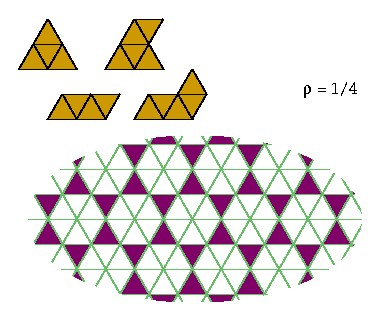
This pattern optimally excludes the V-tetriamond and the U-pentiamond:
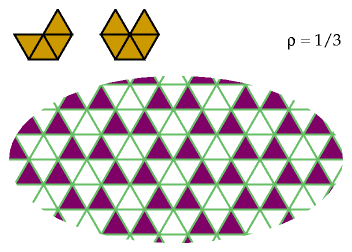
This pattern is the best I have for the I-pentiamond:
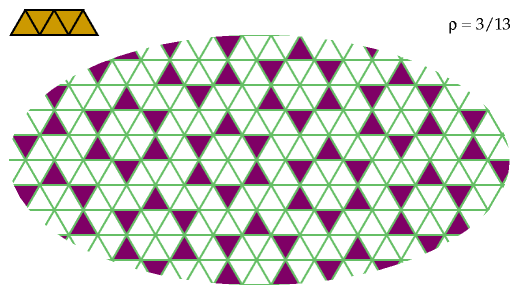
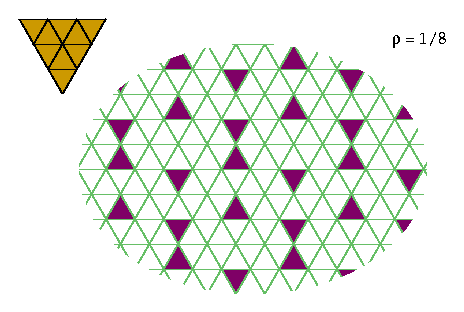
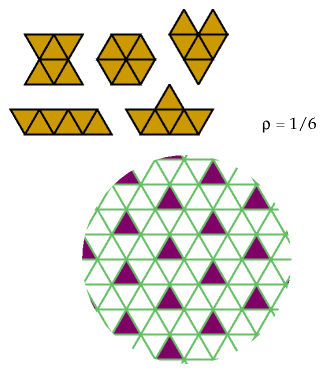
This pattern of holes excludes five hexiamonds:
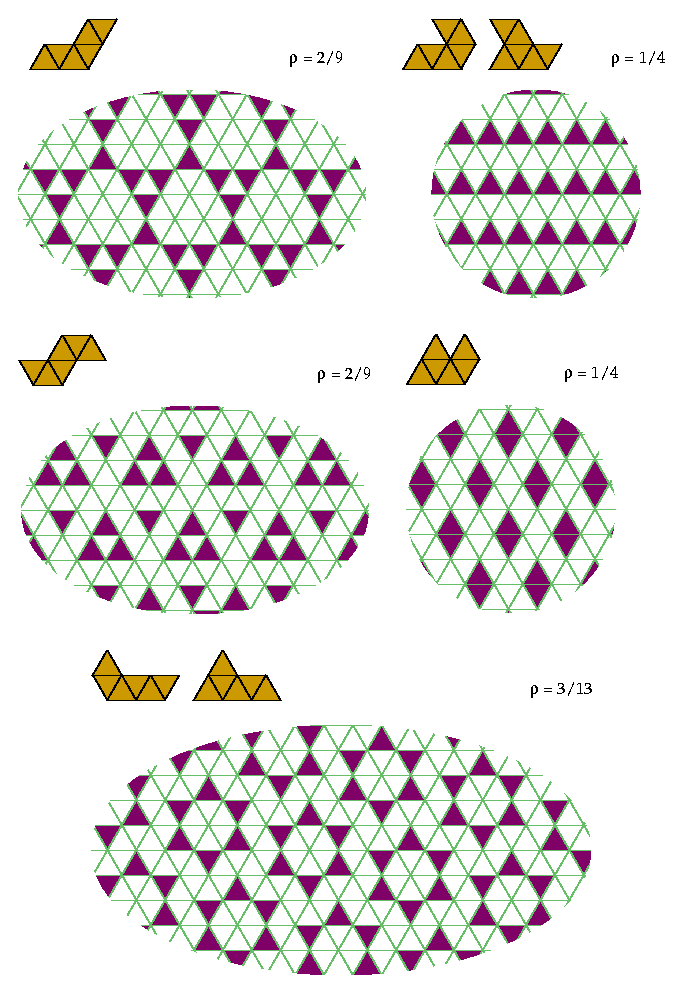
Here are my best results for the other hexiamonds:
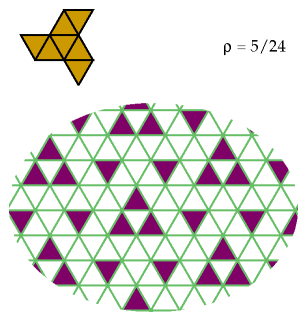
For good measure here is a heptiamond exclusion, not necessarily optimal:
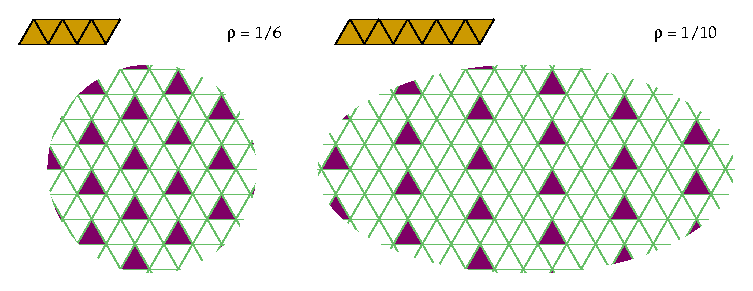
Any straight polyiamond of even order n can be excluded with 1/n holes. You can generalize the following patterns to any n that is twice an odd number by adjusting the distance between the columns of holes:
Similarly, you can generalize the following patterns to any n that is twice an even number. Each column with holes contains n/4 upward holes, then n/4 downward holes, and so on.
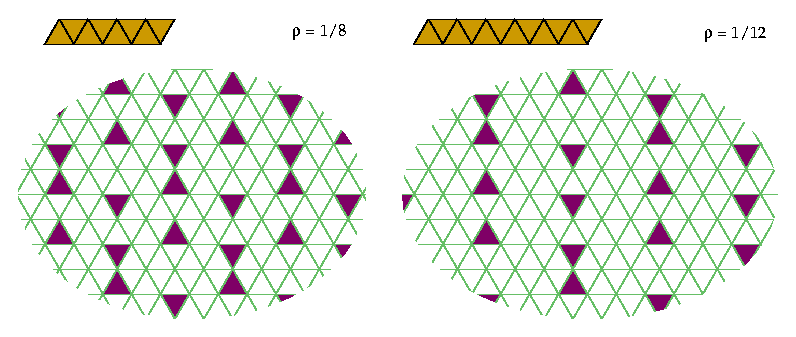
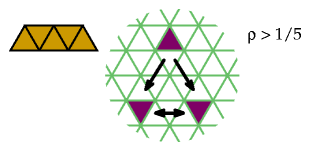
Straight polyiamonds of odd order require more than 1/n holes. If 1/n holes sufficed, then every row would need exactly 1/n holes, for if some rows had more than 1/n, others would have less than 1/n to compensate, which would admit a straight polyiamond of order n. Therefore every row must have a hole just at every nth cell. But if n is odd, this is impossible, as the following diagram illustrates:
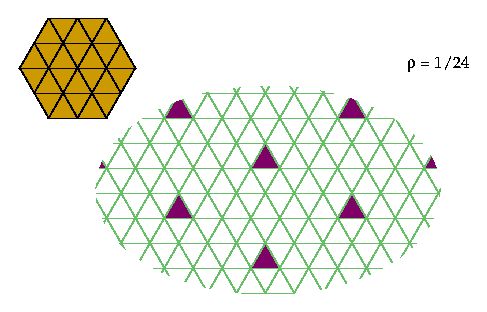
Any regular hexagon can be excluded efficiently:
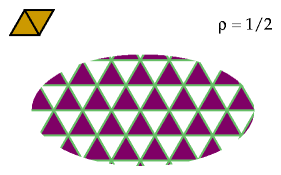
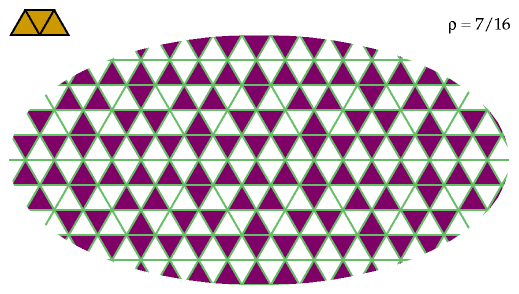
The same is not true of equilateral triangles: