Polyaboloes
The polyaboloes (also known as polytans) are shapes formed by joining half squares (cut diagonally) together. There is one monabolo, three diaboloes, four triaboloes and 14 tetraboloes (see below). For more information on the tetraboloes see Henri Picciotto's site, Michael Keller's Game and Puzzle Pages and Miroslav Vicher's polytans page. Also Peter Esser has an excellent site with a lot of information on polyaboloes. Also Kadon Enterprises makes sets of polyaboloes up to and including the hexaboloes.
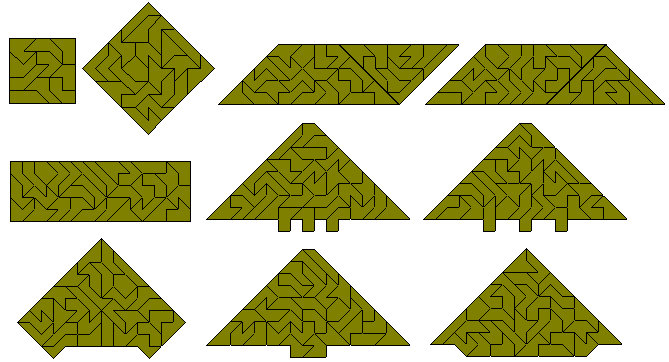
Sets of 2, 3, 5 or 6 congruent shapes can also be made. Notice that the two trapezia could be combined to make the parallelogram, trapzium and rectangle above. Three 5x5 squares would have the required area but cannot be made as the pieces cannot contribute enough to the edges but it is possible to make three triangles as shown here.

The pentaboloes can also be used to make simultaneous one- two- and five-fold copies of one of the pieces. One-, two-, three- and four-fold copies can also be made. The largest number of copies is seven (one- four two- and one three-fold) as shown in the last figure below.
Similar constructions can also be made which include enlargement factors which are multiples of2.

There are 107 hexaboloes. These are shown in the diagram below where they form a square with one piece used twice. The solution at the left was made by hand in the 1960s. The only other known solution is the one at the right made by Anneke Treep in 2001 where the extra piece is placed symmetrically.
Peter Esses has made four triangles with this set using one piece twice.
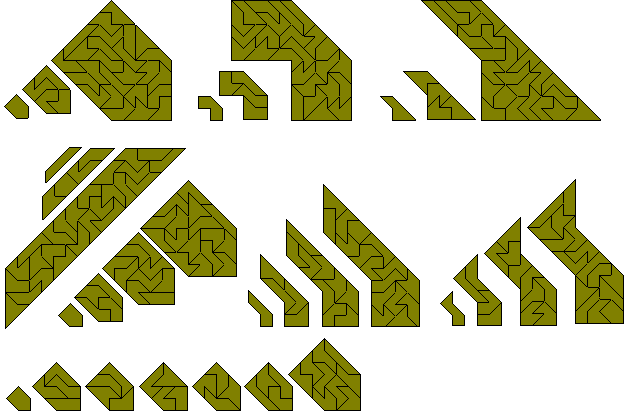
Although the 107 pieces cannot make any rectangle it should be possible to make one-, five- and nine-fold copies of some of the pieces. The pieces to be made must odd numbers of sloping edges in both directions as in the diagrams below by Peter Esser. As Peter points out not only must there be an odd number of sloping edges but also 1-5-9-replicas are possible only for the balanced pieces because there is an odd number of balanced pieces which gives an odd number of black triangles under checkerboard colouring for the whole construction.

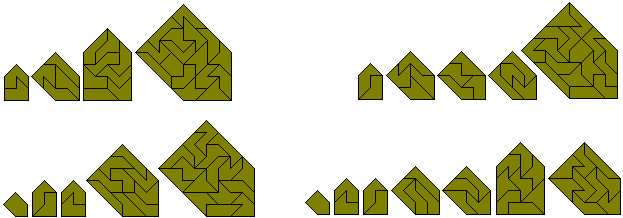
Since the total area of the pentaboloes is 75 square units, it should be possible to form quintuplications of the hexaboles using the set. Five examples are shown below. (Peter Esser's site has solutions for all 107 problems)
One-sided Polyaboloes
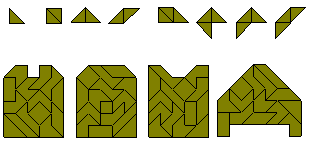
The constructions below are made with the 22 one-sided tetraboloes.
There are 56 one-sided pentaboloes shown in the constructions below where a variety of sets of similar shapes have been made with the pieces. For more one-sided pentabolo constructions see Peter Esser's constructions with the one-sided pentaboloes.
The next diagram shows some sets of congruent shapes made with this set.
The last figure above is an example of a solution to a similar hole problem. Peter Esser has also made a number of similar hole constructions with the one-sided pentaboloes. There are a number of other constructions on Peter's site.