Polyomino Bireptiles

Introduction

In combinatorial geometry a reptile is a geometric figure, equal copies of which can be joined to form an enlarged form of the figure. For example, four copies of the P-pentomino can form a P-pentomino at double scale, or four times as large:

Reptiles are known for polyominoes, polyiamonds, polyaboloes, and other polyforms.

Few polyforms of any kind form reptiles. A bireptile is a figure of which copies can be joined to form two joined, equally enlarged copies of the original figure.

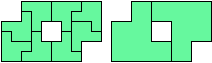
Any figure with a reptiling trivially has a bireptiling, but not every figure with a bireptiling has a reptiling. That is, bireptiles are more common than reptiles.

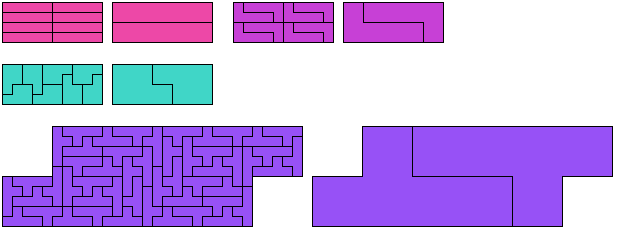
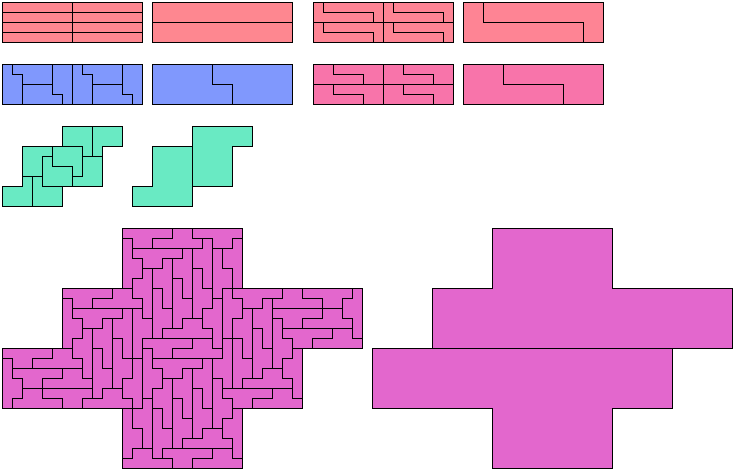
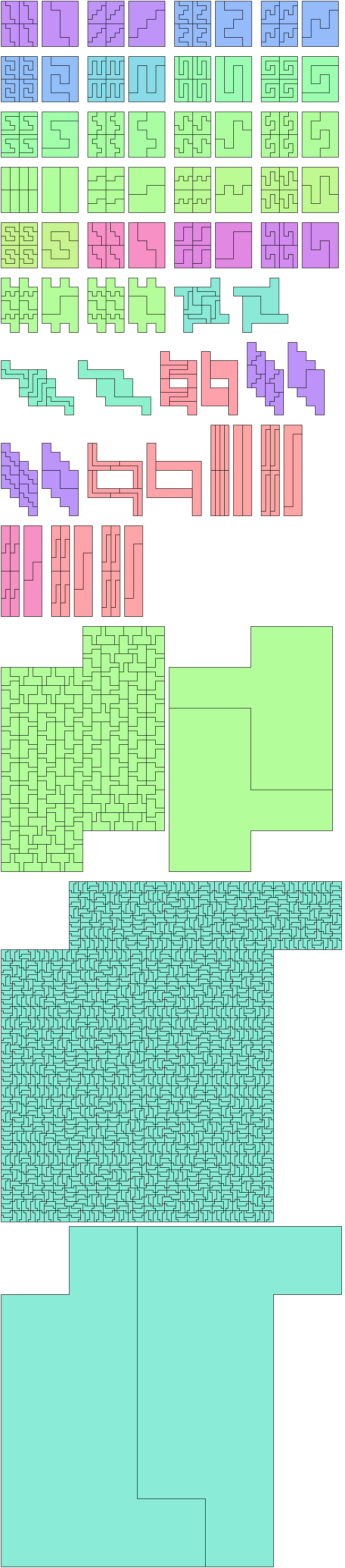
Below I show minimal known bireptilings for various polyominoes.

Number of
Cells		Number of
Reptiles		Number of
Bireptiles
111
211
322
444
544
61011
766
81216
94141
102835

Pentominoes

Hexominoes

Heptominoes

Octominoes

Enneominoes

Decominoes

Last revised 2015-12-10.

Back to Polyform Tiling < Polyform Curiosities
Col. George Sicherman { HOME | MAIL }