

 | Kiteless Didoms. Form shapes with the set of 12 didoms, omitting the kite didom. |
 | Scaled Polydom Tetrads. Join four similar polydoms so that each borders the other three. |
 | Polydom Irreptiling. Dissect a polydom into smaller copies of it, not necessarily equal. |
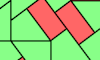 | Didom Kites and Bricks. Livio Zucca's problem of tiling a rectangle with didom kites and dominoes. |
 | A Counterexample To
Livio Zucca's Island Conjecture.
Make a polydom islandin the shape of a polyomino that cannot be tiled with dominoes. |
 | Convex Figures with Didom Pairs. Make a convex polydom with copies of two didoms. |
 | Convex Figures with Didom Triplets. Make a convex polydom with copies of three didoms. |
 | Convex Shapes from the 13 Didoms. Make a convex polydom with the 13 didoms, including the Kite Didom. |
 | Inflated Didoms. Make a convex polydom with the 13 didoms, including the Kite Didom, enlarging some. |
 | Tiling the Owen Dodecagon With Three Didoms. Make an almost regular dodecagon with copies of the 13 didoms. |

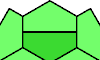
 | Convex Shapes from Scherer Quadrangles. Join copies of the Scherer Quadrangle to make convex shapes. |
 | Contiguous Partridge Tilings. Use 1 shape at scale 1, 2 at scale 2, and so on up to n at scale n, to form a scaled copy of the shape in which equal tiles are contiguous. |
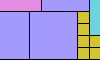 | Contiguous Reverse Partridge Tilings. Use 1 shape at scale n, 2 at scale n−1, and so on up to n at scale 1, to form a scaled copy of the shape in which equal tiles are contiguous. |
 | Lovebirds Tilings. Use 2 copies of a shape at scale 1, 4 at scale 2, and so on up to 2n at scale n, to form two scaled copies of the shape. |
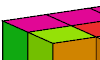 | Wrapping a Heptacube with Trominoids. Tile the surface of a suitable heptacube with the one-sided trominoids, omitting one trominoid that cannot be used. |
 | Polyominoid Möbius Bands. Using as few cells as possible, construct a polyominoid with the structure of a Möbius Band. |