Strong Surround Numbers for Polyaboloes
A polyabolo is a plane figure formed by
joining equal isosceles right triangles along equal edges.
The strong surround number of a polyabolo
is the fewest number of copies of the polyabolo that can surround
it strongly; that is, including its corners.
The polyaboloes must conform to the quadrille grid.
Strong surround numbers for polyominoes were proposed
by Jaime Poniachik in Issue 8
of Puzzle Fun.
He asked for the smallest polyominoes with a given strong surround number.
In Issue 10,
Rodolfo Kurchan extended the problem
to polyiamonds, polyhexes, and polyaboloes.
He also investigated the smallest polyforms that cannot surround themselves,
and the smallest holeless such polyforms.
However, his results were not complete.
Here I show minimal strong surrounds for small polyaboloes,
the smallest polyaboloes with given surround numbers,
and the smallest polyaboloes with no strong surrounds.
See also Strong Surround Numbers
for Polycairos.
Minimal Strong Surrounds
Monabolo

Diaboloes
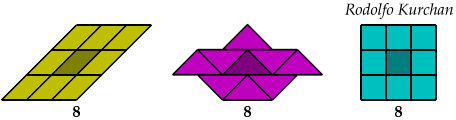
Triaboloes
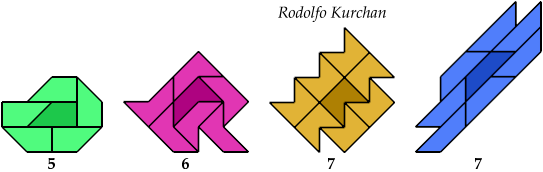
Tetraboloes
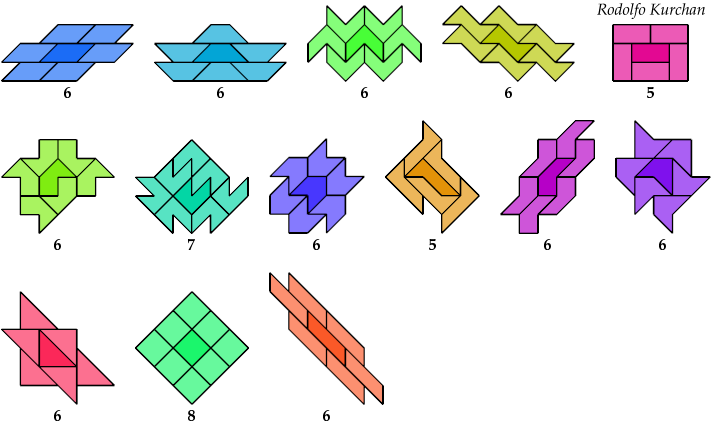
Minimal Polyaboloes with Given Strong Surround Numbers
3 Copies, 16 Cells
These solutions were found by Juris Čerņenoks.
4 Copies, 6 Cells
The second solution was found by Rodolfo Kurchan.

5 Copies, 3 Cells
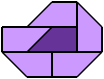
6 Copies, 3 Cells

7 Copies, 3 Cells
The second solution was found by Rodolfo Kurchan.
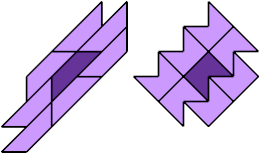
8 Copies, 2 Cells
The first solution was found by Rodolfo Kurchan.
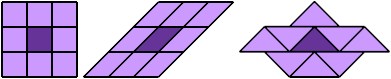
9 Copies, 7 Cells

10 Copies, 1 Cell
This solution was found by Rodolfo Kurchan.
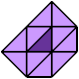
11 Copies, 9 Cells

12 Copies, 9 Cells

13 Copies, 11 Cells
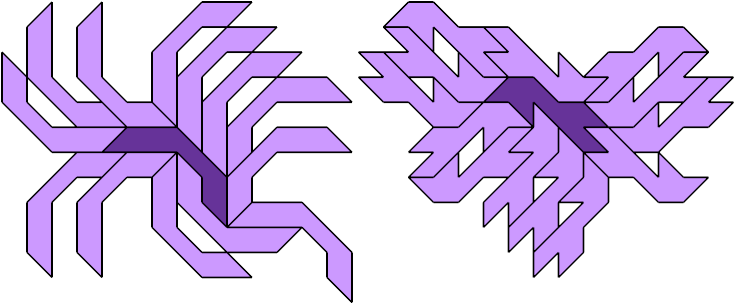
14 Copies, 10 Cells

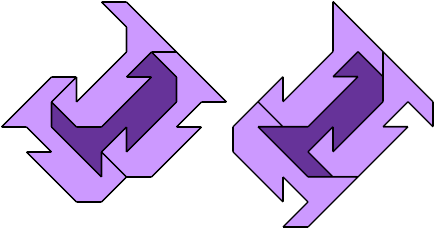
Minimal Polyaboloes that Cannot Surround Themselves Strongly
The fourth solution was found by Rodolfo Kurchan.

Last revised 2022-08-14.
Back to Polyform Tiling
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]

















