Pentacubes in a Box With Four Edges Removed

Introduction

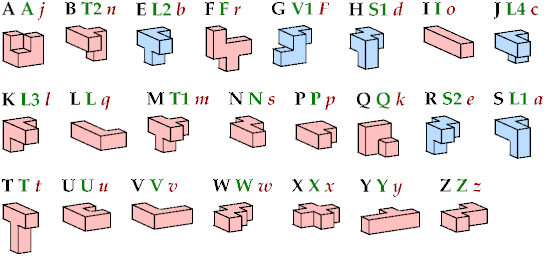
The six blue tiles have distinct mirror images. Kate Jones's names are shown in green. Donald Knuth's names are shown in red.

In Kate Jones's nomenclature and mine, flat pentacubes bear Solomon Golomb's names for the corresponding pentominoes. In Donald Knuth's nomenclature, flat pentacubes bear John Conway's names for the corresponding pentominoes.

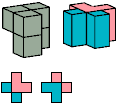
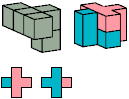
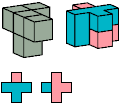
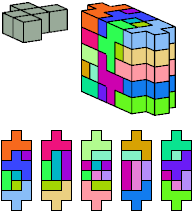
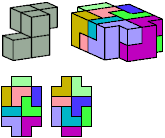
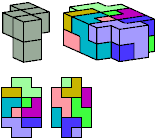
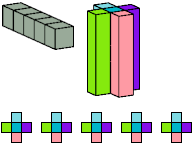
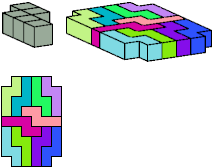
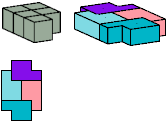
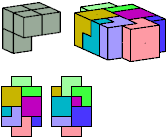
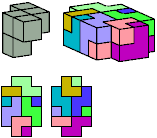
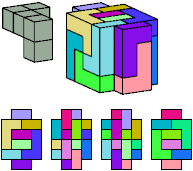
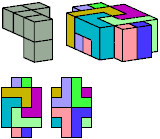
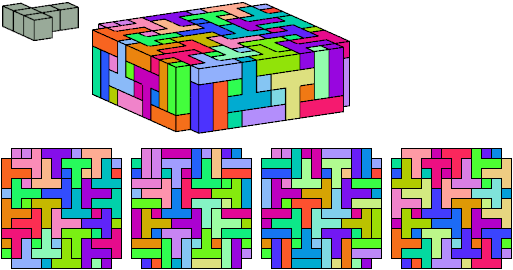
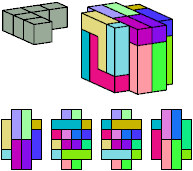
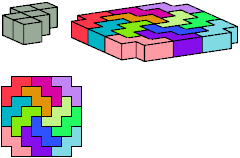
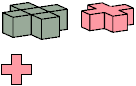
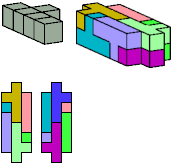
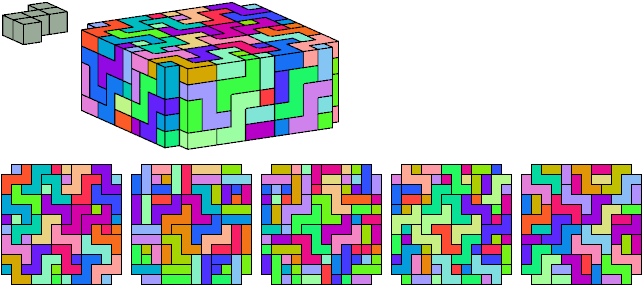
All but two pentacubes can tile a rectangular prism, or box; see Pentacubes in a Box. Here I show that every pentacube can tile a box from which the cells along four parallel edges have been removed. Dimensions are given with the height last. The cross-sections are shown from top to bottom. If you find a smaller solution for a pentacube, please write.

Solutions

A

B

E

F

G

H

I

J

K

L

M

N

P

Q

R

S

With Reflection

T

U

V

W

X

Y

Z

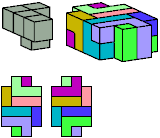
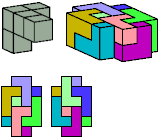
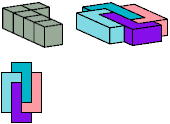
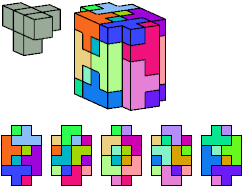
Last revised 2022-03-03.