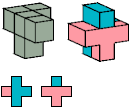Pentacubes in a Box Without Corners
Introduction
A pentacube is a solid made of five equal cubes joined
face to face.
There are 23 such figures, not distinguishing reflections and rotations:
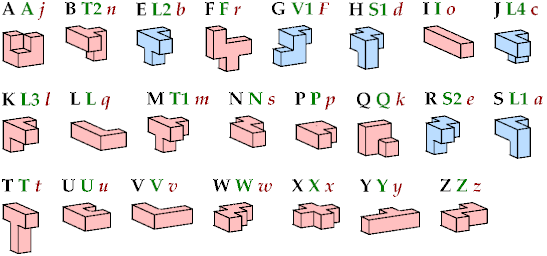
The six blue tiles have distinct mirror images.
Kate Jones's systematic names are shown in green.
Donald Knuth's names are shown in red.
All but two pentacubes can tile a rectangular prism, or box;
see Pentacubes in a Box.
Here I show that every pentacube can tile a box with the corner cells
removed.
The cross-sections are shown from back to front.
If you find a smaller solution for a pentacube, please write.
Solutions
A
2 tiles, 2×3×3
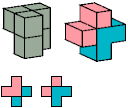
B
2 tiles, 2×3×3
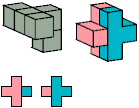
E
2 tiles, 2×3×3
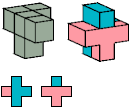
F
20 tiles, 3×6×6
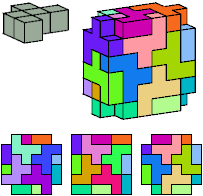
G
8 tiles, 2×4×6
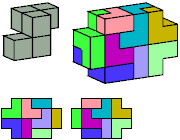
H
8 tiles, 3×4×4
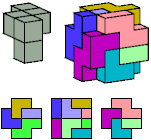
I
9 tiles, 1×7×7
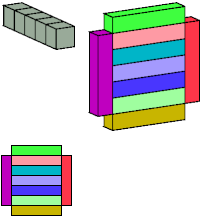
J
8 tiles, 2×4×6
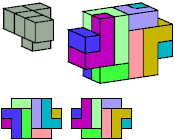
K
8 tiles, 2×4×6
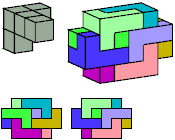
L
4 tiles, 1×4×6
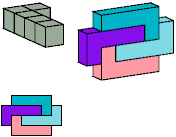
M
312 tiles, 7×8×28
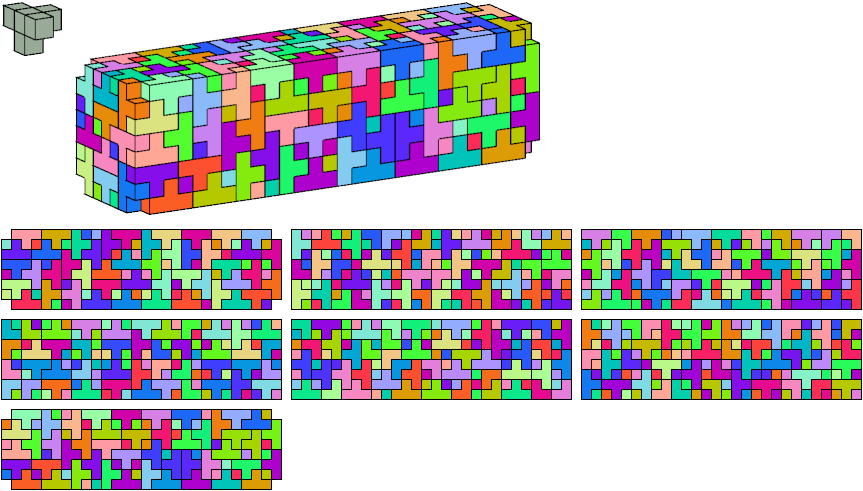
N
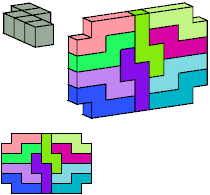
10 tiles, 1×6×9
P
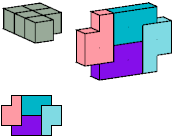
4 tiles, 1×4×6
Q
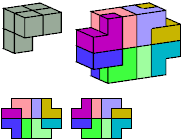
8 tiles, 2×4×6
R
8 tiles, 2×4×6
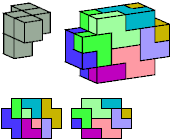
S
With Reflection
8 tiles, 2×4×6
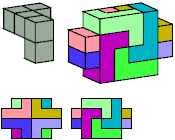
Without Reflection
248 tiles, 6×8×26
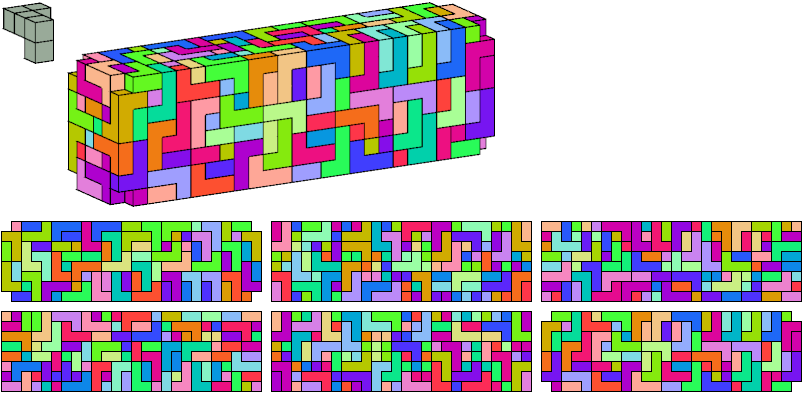
T
92 tiles, 3×12×13
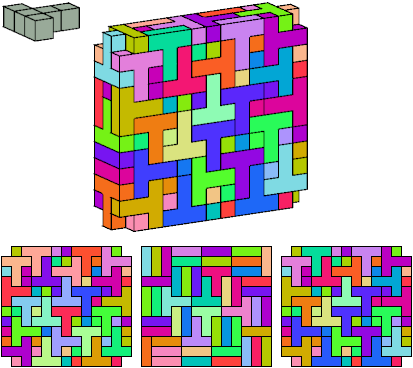
U
2 tiles, 2×3×3
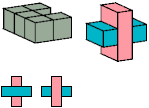
V
56 tiles, 6×6×8
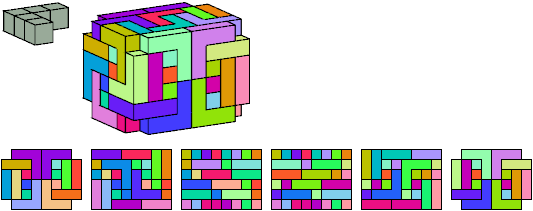
W
12 tiles, 1×8×8
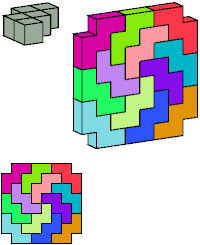
X
1 tile, 1×3×3
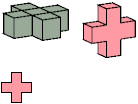
Y
8 tiles, 2×3×8
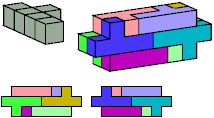
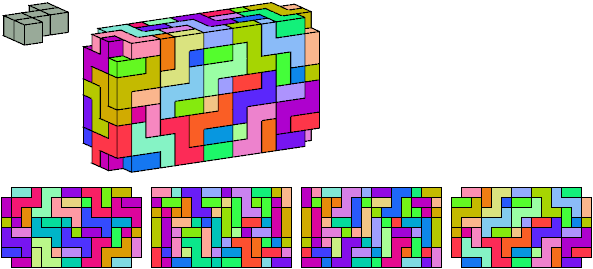
Z
88 tiles, 4×8×14
Last revised 2016-02-10.
Back to Polyform Tiling
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]