
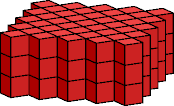
A diamond polyomino is a polyomino in the form of an oblique
square
with four zigzag edges.
A diamond prism polycube
is a polycube prism whose base is a diamond polyomino.
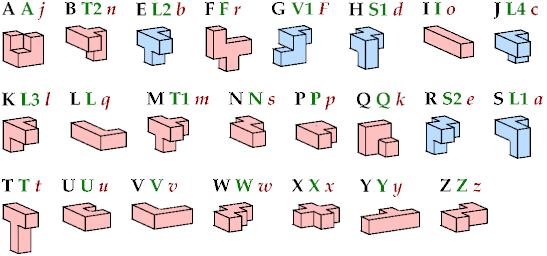
Here I show the smallest known diamond prism polycubes that can be tiled with copies of of two different pentacubes, using at least one of each. A prime mark (′) after a letter denotes a mirror image. For example, S′ is the mirror image of S. To see a tiling, click on the corresponding entry in the table below. Missing entries indicate unsolved cases.
If you find a smaller solution, or solve an unsolved case, please write.
See also Tiling Triangular Prism Polycubes with Two Pentacubes and Tiling Pyramid Prism Polycubes with Two Pentacubes.
| A | B | E | E′ | F | G | G′ | H | H′ | I | J | J′ | K | L | M | N | P | Q | R | R′ | S | S′ | T | U | V | W | X | Y | Z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 4 | 4 | 10 | 10 | 10 | 7 | 4 | 10 | 4 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 4 | 10 | 10 | 3 | 4 | 10 | |||||||
| B | 3 | 10 | 3 | 10 | 7 | 6 | 15 | 6 | 13 | 10 | 10 | 10 | 10 | 13 | 5 | 4 | 4 | 10 | 3 | 6 | 5 | ||||||||
| E | 4 | 10 | 3 | 10 | 10 | 10 | 7 | 4 | 4 | 20 | 6 | – | 10 | 10 | 10 | 10 | 10 | 25 | 15 | 3 | 4 | 15 | 10 | 3 | 6 | 4 | |||
| F | 20 | 34 | 13 | 15 | 34 | 20 | 106 | 17 | 17 | 34 | 34 | 34 | 17 | 10 | 20 | 17 | 5 | 20 | 29 | ||||||||||
| G | – | 25 | 34 | 26 | 15 | 3 | 20 | 20 | – | 20 | 20 | 20 | – | – | – | 30 | 30 | 10 | 3 | 20 | 10 | 20 | 34 | ||||||
| H | 34 | 13 | 15 | 15 | 34 | 20 | 34 | 34 | 34 | 34 | 34 | 34 | 34 | 34 | 30 | 10 | 15 | 34 | 10 | 20 | 34 | ||||||||
| I | 13 | 6 | 5 | 25 | 13 | 5 | 13 | 25 | 25 | 6 | 7 | 13 | 13 | 6 | 13 | 13 | |||||||||||||
| J | 15 | 15 | 15 | 20 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 3 | 15 | 15 | 15 | 20 | 4 | 15 | |||||||||||
| K | 20 | – | – | – | 34 | 34 | – | 51 | 30 | – | 34 | 68 | 20 | – | |||||||||||||||
| L | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 4 | 20 | 17 | 20 | 4 | 20 | ||||||||||||||||
| M | – | – | 34 | – | – | – | 15 | – | 34 | – | 13 | – | |||||||||||||||||
| N | – | 34 | 34 | 34 | 30 | 30 | 20 | 17 | 41 | 20 | – | ||||||||||||||||||
| P | 34 | 34 | 34 | 20 | 15 | 15 | 17 | 15 | 17 | 20 | |||||||||||||||||||
| Q | 34 | 34 | 20 | 10 | 20 | 34 | 10 | 20 | 34 | ||||||||||||||||||||
| R | – | 34 | – | 51 | 10 | 30 | 34 | 10 | 20 | 34 | |||||||||||||||||||
| S | – | 51 | 30 | 20 | 34 | – | 20 | – | |||||||||||||||||||||
| T | 20 | 51 | 51 | – | 75 | – | |||||||||||||||||||||||
| U | 4 | 10 | 3 | 4 | 51 | ||||||||||||||||||||||||
| V | 20 | 30 | 4 | 51 | |||||||||||||||||||||||||
| W | 5 | 13 | 17 | ||||||||||||||||||||||||||
| X | 68 | – | |||||||||||||||||||||||||||
| Y | 20 | ||||||||||||||||||||||||||||
| Z | |||||||||||||||||||||||||||||
Last revised 2024-02-08.