Pentacubes in a Box With All Edges Removed

Introduction

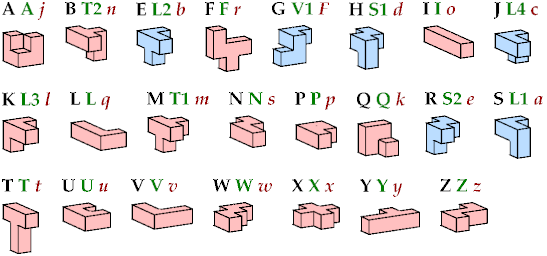
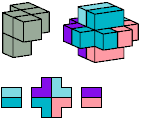
The six blue tiles have distinct mirror images. Kate Jones's names are shown in green. Donald Knuth's names are shown in red.

In Kate Jones's nomenclature and mine, flat pentacubes bear Solomon Golomb's names for the corresponding pentominoes. In Donald Knuth's nomenclature, flat pentacubes bear John Conway's names for the corresponding pentominoes.

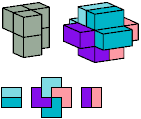
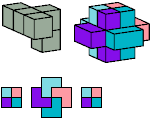
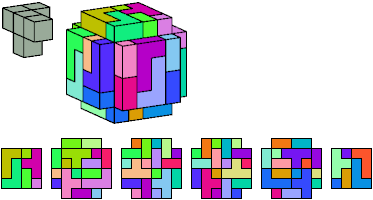
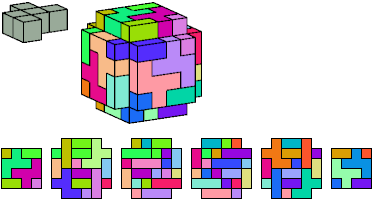
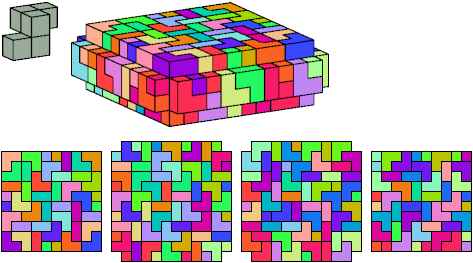
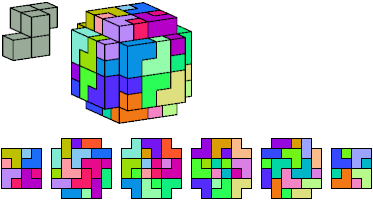
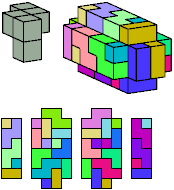
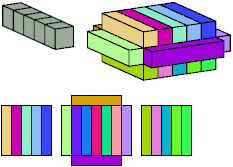
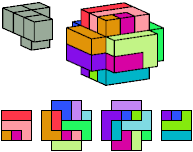
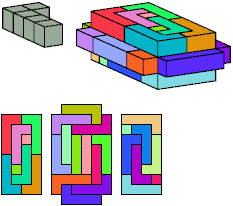
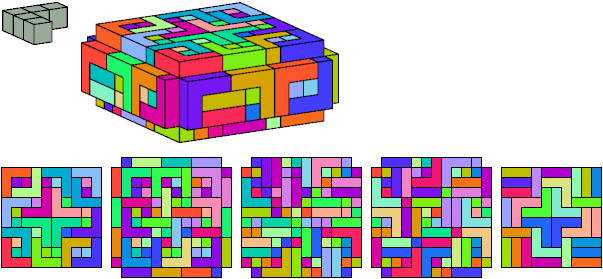
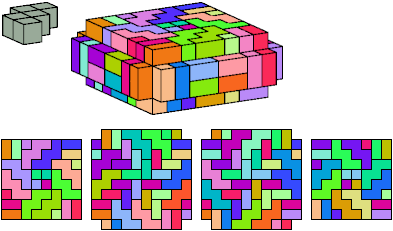
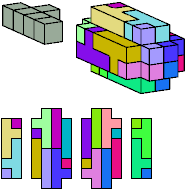
All but two pentacubes can tile a rectangular prism, or box; see Pentacubes in a Box. Here I show, for each pentacube, a minimal known box from which the cells along all edges have been removed, tiled by that pentacube. The cross-sections are shown from top to bottom. If you find a smaller solution for a pentacube, or solve an unsolved case, please write.

Solutions

A

B

E

F

G

With Reflection

H

I

J

K

L

M

N

P

Q

R

S

With Reflection

T

U

V

W

X

Y

Z

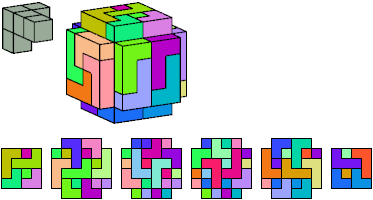
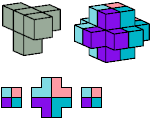
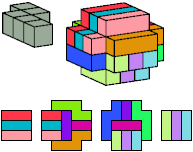
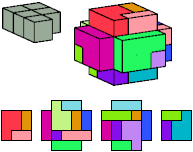
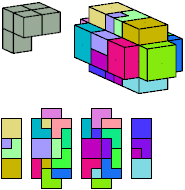
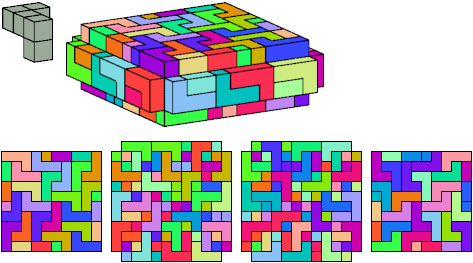
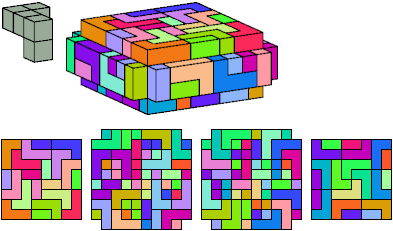
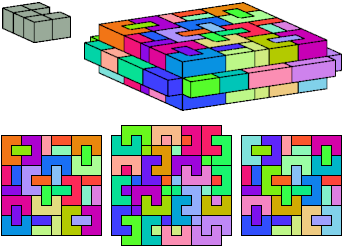
Last revised 2022-03-04.