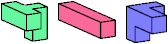
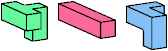
| BIK | BIS (BIS′) | FGX (FG′X) | FGZ (FG′Z) |
|---|---|---|---|
| 
| 
| 
|
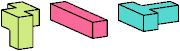
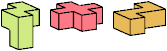
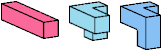
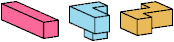
| HIT (H′IT) | HXZ (H′XZ) | IJS (IJ′S′) | IJZ (IJ′Z) |
| 
| 
| 
|
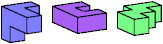
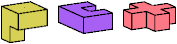
| IRT (IR′T) | IRZ (IR′Z) | KUW | QUX |

| 
| 
| 
|
| RSX (R′S′X) | |||
|
The number of pentacube triples, or sets of three different pentacubes, is C(29, 3), or 3654. Most of these triples can be joined to form symmetric 15-cubes. These 39 cannot: AFI, AIS/AIS′, AIT, ASX/AS′X, ATX, FGI/FG′I, GIK/G′IK, GKX/G′KX, HIX/H′IX, HIZ/H′IZ, IEV/IE′V, IJW/IJ′W, IJX/IJ′X, IKS/IKS′, IKU, IQT, IQZ, IRX/IR′X, JXZ/J′XZ, KLX, QTX, QXZ, RTX/R′TX, RXZ/R′XZ.
At the other extreme, the triple BLN can form 27086 different symmetric polycubes!
Just 23 triples have unique solutions. These triples are shown below. To see a solution, click on the triple. Cross-sections are shown from top to bottom.
| BIK | BIS (BIS′) | FGX (FG′X) | FGZ (FG′Z) |
|---|---|---|---|

| 
| 
| 
|
| HIT (H′IT) | HXZ (H′XZ) | IJS (IJ′S′) | IJZ (IJ′Z) |

| 
| 
| 
|
| IRT (IR′T) | IRZ (IR′Z) | KUW | QUX |

| 
| 
| 
|
| RSX (R′S′X) | |||

|
I am indebted to Gál Péter for his investigation of symmetric pentacube pairs.