Many heptacubes can fill three-dimensional space, especially if we let them be reflected; that is, if we use both a heptacube and its mirror image.
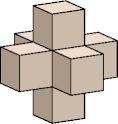
The pansymmetric heptacube is the only heptacube with full cubical symmetry:

It is well known that the pansymmetric pentomino, the X-pentomino, can fill two-dimensional space:

It is not generally known that the pansymmetric heptacube can fill three-dimensional space. The method is shown below.
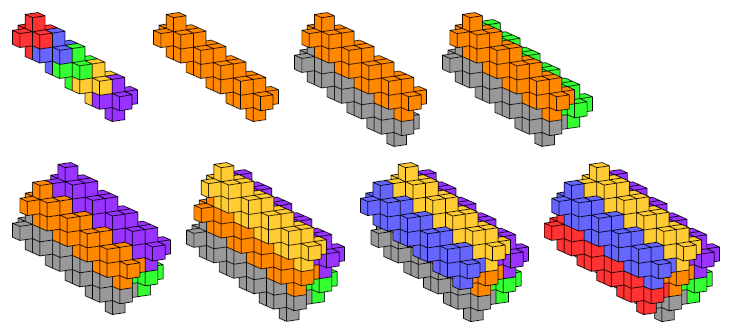
The first figure shows pansymmetric heptacubes joined to form an infinite straight diagonal row. The remaining figures show how six of these rows can surround a seventh row, the orange row. Repeating this process for every row will fill space with copies of the pansymmetric heptacube.
Thanks to Donald Bell for suggesting that I illustrate this construction.
Last revised 2020-04-24.