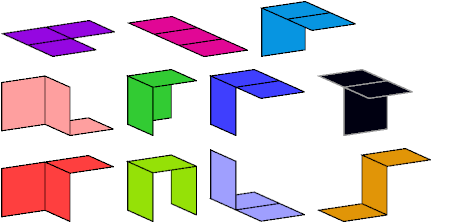

A set of polyominoids is said to wrap a polycube if it tiles the polycube's surface. The black trominoid shown above has three cells incident at a common edge. It can be used in wrapping only rare polycubes, such as the A pentacube:
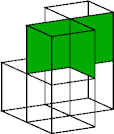
The surface area of every polycube is an even number. The total area of 11 trominoids is 33. They cannot wrap a polycube.
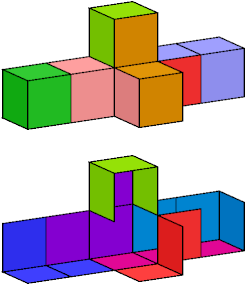
If we exclude the forked trominoid, the remaining 10 trominoids can wrap any of 269 heptacubes. However, 73 heptacubes can be wrapped with the forked trominoid and 9 others. They include the heptacube with a hole shown below.
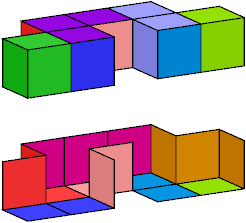
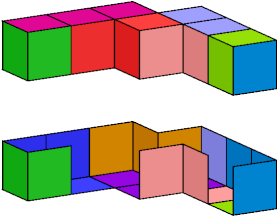
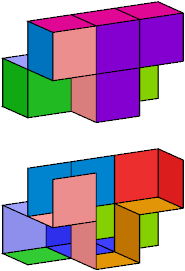
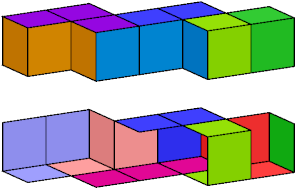
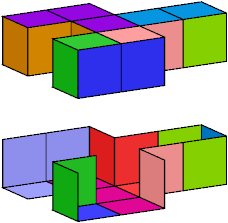
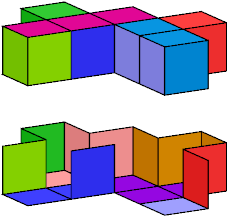
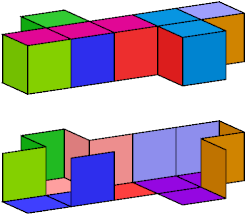
Here I show wrappings without the forked trominoid for 9 heptacubes with compound symmetry. In each image, the lower figure is a cutaway picture. An exclamation point (!) means that the tiling is unique up to rotation and reflection.
 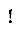
|  
|  
|
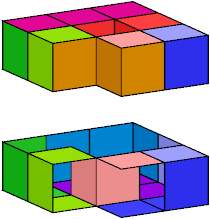 
| 
|  
|
| 
| 
|
The 10 usable trominoids can also wrap 81 octacubes and one enneacube.
Last revised 2025-09-26.