The Lobster and the Snake: Four Puzzles

Introduction

A hexiamond is a plane figure made of six equilateral triangles joined edge to edge. There are 12 such figures, not distinguishing reflections and rotations. They were first enumerated by T. H. O'Beirne.

The two hexiamonds shown above are often called the Lobster and the Snake. These creatures have a curious relationship! Here I present four puzzles about them.

A Fable

Martin Watson has suggested that this page would be improved by a brief story. I am happy to oblige him.

A Lobster walking on the seabed saw a Sea Snake approaching. Good day to you, friend Snake, said the Lobster, extending its claws. Will you not swim closer? I have long wondered whether Snake is good to eat.
Not nearly as good as Lobster, the Snake answered, showing its fangs.
MORAL: One may receive a compliment and yet not be pleased.

Growing Up Alike

Attach copies of the same polyiamond to the Lobster and the Snake so that the resulting shapes are identical.

For example, we can attach a triamond (yellow) to these two other hexiamonds so that the resulting shapes are identical:

For full credit, use the smallest possible polyiamond.

Filling Out

Arrange copies of the Lobster and the Snake, at least one of each, to make a convex polyiamond.

A shape is convex if any two points inside it can be joined by a straight line that also lies inside it. In practice, this means that the shape has no holes or indentations.

For example, this convex shape is made from copies of two other hexiamonds:

For full credit, use the smallest possible polyiamond.

Sister Act

Find a polyiamond that can be tiled by the Lobster, and also by the Snake.

For example, these two other hexiamonds can independently tile the same polyiamond:

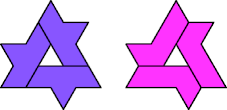
For full credit, use the smallest possible polyiamond.

Odd Couple

Arrange an odd total number of Lobsters and Snakes to form a polyiamond with full (snowflake) symmetry.

For example, 7 copies of these two other hexiamonds can form a polyiamond with full symmetry:

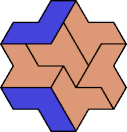
For full credit, use the smallest possible polyiamond.

{ SOLUTIONS }

Last revised 2020-08-02.

Back to Polyiamond and Polyming Tiling < Polyform Tiling < Polyform Curiosities

Col. George Sicherman [ HOME | MAIL ]