
A trapezium is a quadrilateral with just two sides parallel. In the U.S. and Canada it is usually called a trapezoid, and a quadrilateral with no sides parallel is called a trapezium. The confusion appears to have arisen from a popular 18th-century English dictionary of mathematics that mixed up the two terms.
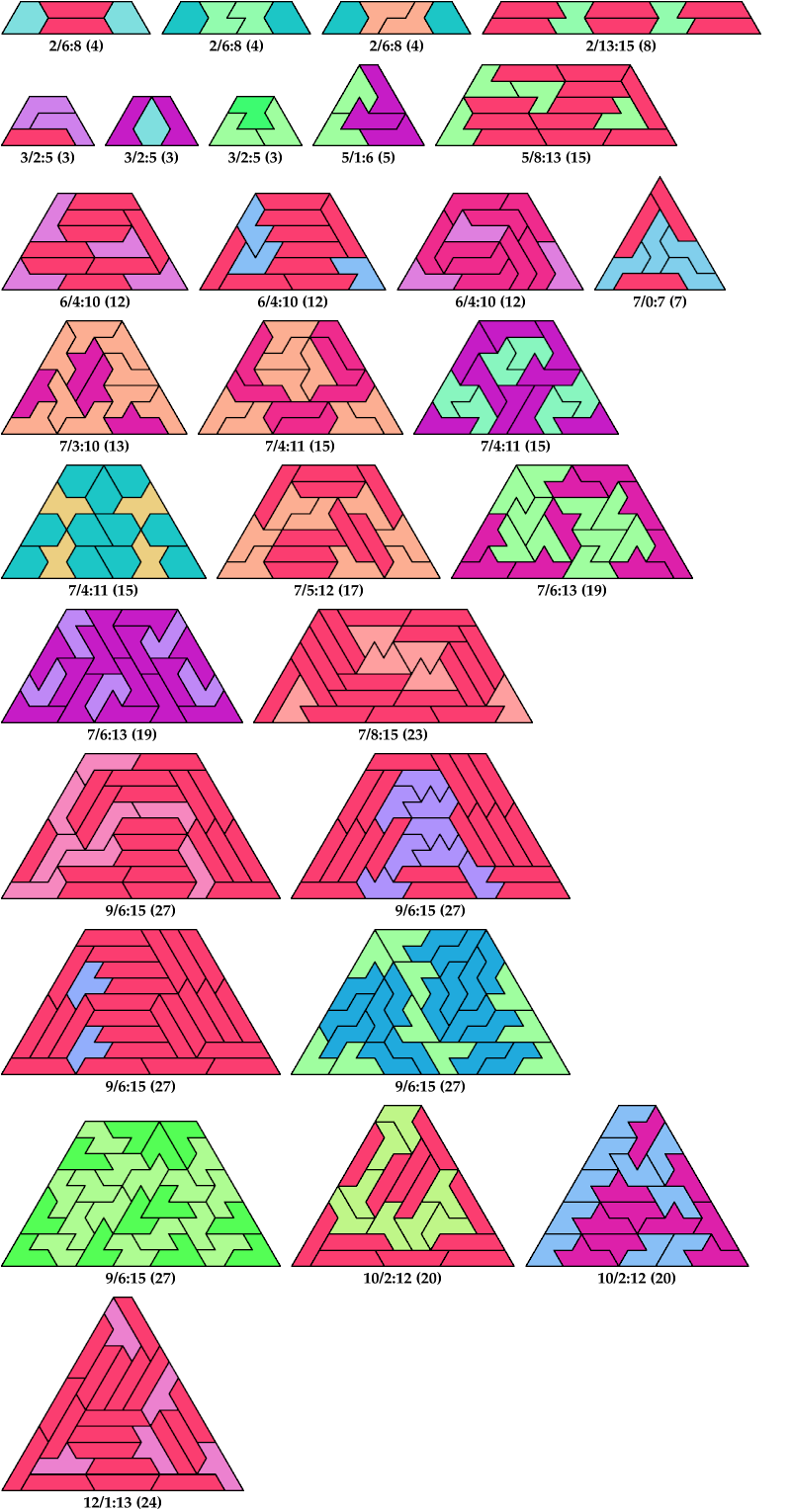
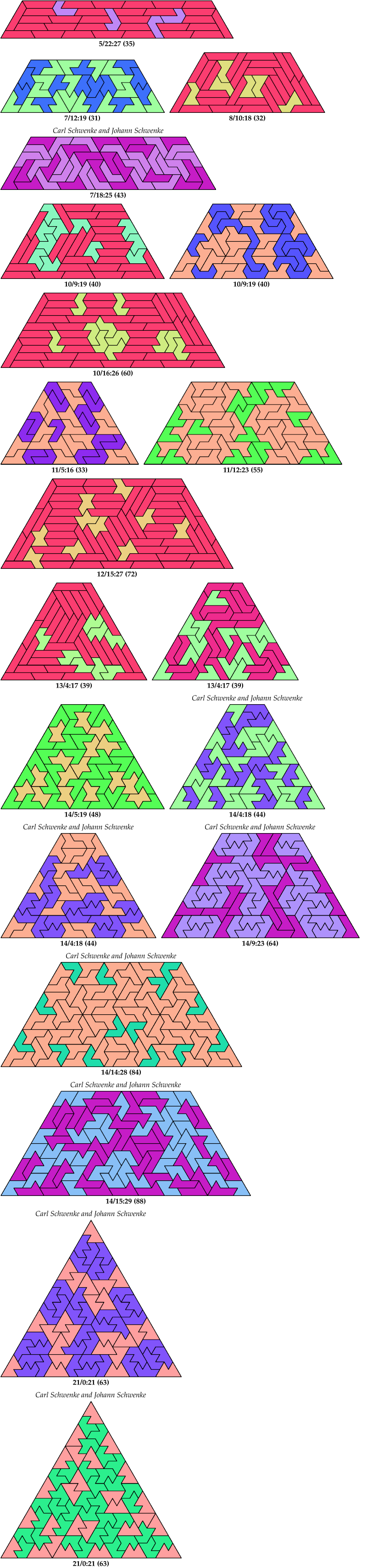
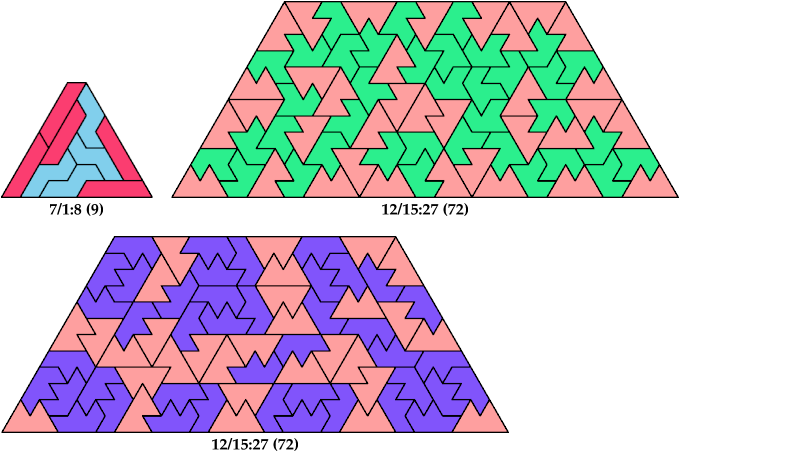
Here I show the smallest known trapezia that can be formed by copies of two heptiamonds, using at least one of each. I allow triangles as a special case of trapezia. If you find a smaller solution or solve an unsolved pair, please write.
Carl Schwenke and Johann Schwenke found new solutions and improvements.
See also
Carl Schwenke and Johann Schwenke found the biggest solutions shown here.
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | P | Q | R | S | T | U | V | X | Y | Z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | * | ? | ? | ? | ? | ? | ? | ? | 40 | ? | ? | 15 | 63 | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? |
| B | ? | * | ? | 4 | ? | ? | 3 | ? | 8 | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? |
| C | ? | ? | * | ? | ? | ? | ? | ? | 3 | ? | ? | 43 | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? |
| D | ? | 4 | ? | * | ? | ? | ? | 4 | 4 | ? | 15 | 3 | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? |
| E | ? | ? | ? | ? | * | ? | 19 | 13 | 24 | ? | ? | ? | ? | 20 | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? |
| F | ? | ? | ? | ? | ? | * | 44 | 44 | 27 | ? | ? | 64 | 63 | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? |
| G | ? | 3 | ? | ? | 19 | 44 | * | 55 | 15 | ? | 48 | 5 | ? | ? | ? | ? | 39 | 27 | ? | ? | ? | ? | 31 | 27 |
| H | ? | ? | ? | 4 | 13 | 44 | 55 | * | 17 | 33 | ? | ? | ? | ? | ? | ? | 15 | ? | ? | 40 | 84 | ? | ? | ? |
| I | 40 | 8 | 3 | 4 | 24 | 27 | 15 | 17 | * | 35 | 72 | 12 | 23 | 12 | 60 | 32 | 27 | 7 | 20 | 1209 | 264 | 188 | 27 | 39 |
| J | ? | ? | ? | ? | ? | ? | ? | 33 | 35 | * | ? | 19 | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? |
| K | ? | ? | ? | 15 | ? | ? | 48 | ? | 72 | ? | * | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? |
| L | 15 | ? | 43 | 3 | ? | 64 | 5 | ? | 12 | 19 | ? | * | ? | 88 | ? | ? | 12 | ? | ? | ? | ? | ? | ? | ? |
| M | 63 | ? | ? | ? | ? | 63 | ? | ? | 23 | ? | ? | ? | * | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? |
| N | ? | ? | ? | ? | 20 | ? | ? | ? | 12 | ? | ? | 88 | ? | * | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? |
| P | ? | ? | ? | ? | ? | ? | ? | ? | 60 | ? | ? | ? | ? | ? | * | ? | ? | ? | ? | ? | ? | ? | ? | ? |
| Q | ? | ? | ? | ? | ? | ? | ? | ? | 32 | ? | ? | ? | ? | ? | ? | * | ? | ? | ? | ? | ? | ? | ? | ? |
| R | ? | ? | ? | ? | ? | ? | 39 | 15 | 27 | ? | ? | 12 | ? | ? | ? | ? | * | ? | ? | ? | ? | ? | ? | ? |
| S | ? | ? | ? | ? | ? | ? | 27 | ? | 7 | ? | ? | ? | ? | ? | ? | ? | ? | * | ? | ? | ? | ? | ? | ? |
| T | ? | ? | ? | ? | ? | ? | ? | ? | 20 | ? | ? | ? | ? | ? | ? | ? | ? | ? | * | ? | ? | ? | ? | ? |
| U | ? | ? | ? | ? | ? | ? | ? | 40 | 1209 | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | * | ? | ? | ? | ? |
| V | ? | ? | ? | ? | ? | ? | ? | 84 | 264 | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | * | ? | ? | ? |
| X | ? | ? | ? | ? | ? | ? | ? | ? | 188 | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | * | ? | ? |
| Y | ? | ? | ? | ? | ? | ? | 31 | ? | 27 | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | * | ? |
| Z | ? | ? | ? | ? | ? | ? | 27 | ? | 39 | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | * |



The I and U heptiamonds can form a parallelogram with sides 8 and 21:
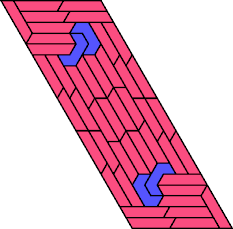
This parallelogram can be joined to the trapezium to make a new trapezium with bases 191 and 212, tiled with both the I and U heptiamonds.
Last revised 2025-04-06.