Tiling a Badge with a Pentiamond and a Heptiamond

Introduction

A pentiamond is a plane figure formed by joining 5 equal equilateral triangles edge to edge. A heptiamond is a plane figure formed by joining 7 equal equilateral triangles edge to edge.

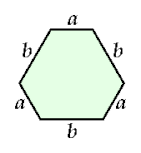
A polyiamond badge is a six-sided polyiamond whose alternate sides have equal length. It is a truncated equilateral triangle. A regular hexagon and an equilateral triangle are special cases of badges.

Here I show the smallest known badges that can be tiled by copies of a given pentiamond and heptiamond, using at least one of each. If you find a smaller solution or solve an unsolved case, please write.

Carl Schwenke and Johann Schwenke contributed smaller solutions.

See also:

  • Tiling a Triangle with a Pair of Polyiamonds

    • 22 Cells

    24 Cells

    33 Cells

    36 Cells

    37 Cells

    46 Cells

    54 Cells

    61 Cells

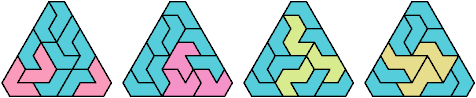
    69 Cells

    73 Cells

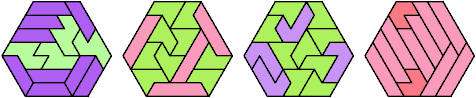
    78 Cells

    81 Cells

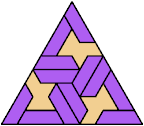
    88 Cells

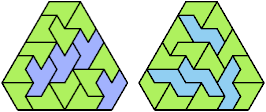
    96 Cells

    100 Cells

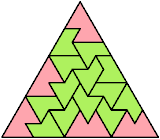
    109 Cells

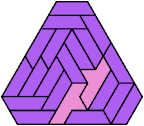
    117 Cells

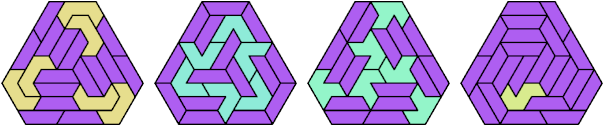
    121 Cells

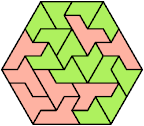
    132 Cells

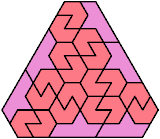
    148 Cells

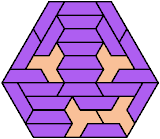
    150 Cells

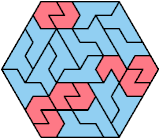
    177 Cells

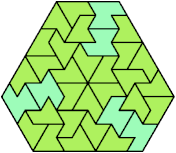
    198 Cells

    216 Cells

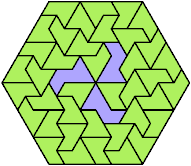
    249 Cells

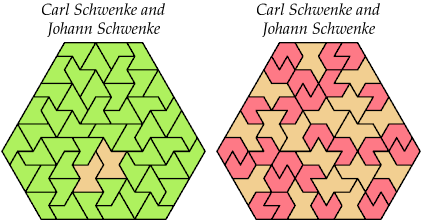
    297 Cells

    384 Cells

    537 Cells

    708 Cells

    Last revised 2025-05-20.

    Back to Tiling a Badge With a Pair of Polyiamonds < Polyiamond and Polyming Tiling < Polyform Tiling < Polyform Curiosities
    Col. George Sicherman [ HOME | MAIL ]