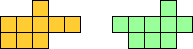

In 2019 Victor Stok asked for the smallest polyominoes that contain every pair of distinct polyominoes. Odette De Meulemeester published the problem at KSO Glorieux's Pentomino site, along with Aad van de Wetering's unique minimal solution.
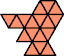
A hexiamond is a plane figure formed by joining six equal equilateral triangles edge to edge. Here are the smallest polyiamonds that contain every pair of distinct hexiamonds. Each has 17 cells. Click on a figure to see how the pairs fit into it.

| 
| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
| |

| 
| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
|
Last revised 2019-10-31.