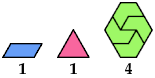
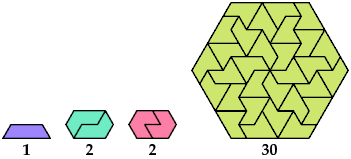
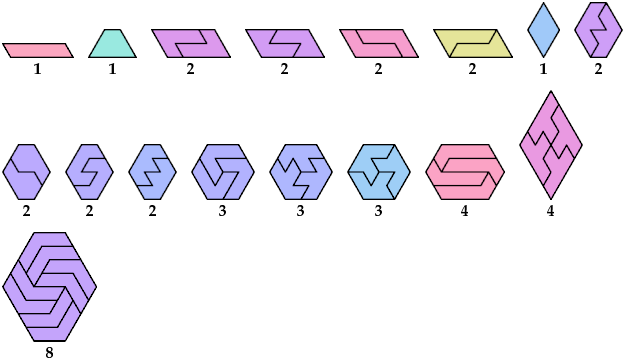
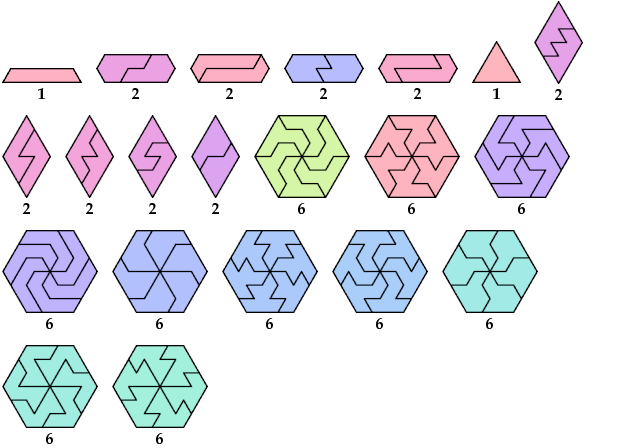
Here I show minimal known convex tilings for polyiamonds with up through 9 cells. If you find a smaller solution or solve an unsolved case, please write.
At Math Magic for April 1999, Erich Friedman considers for various plane shapes the set of values of n for which n copies of the shape can form a convex shape. Ed Pegg Jr. also considers this problem at Dissections of Convex Figures.
See also Convex Polygons from Pairs of Polyiamonds.
[ Diamond | Triamond | Tetriamonds | Pentiamonds | Hexiamonds | Heptiamonds | Octiamonds | Enneiamonds ]






Last revised 2022-04-24.