
It has long been known that only four pentominoes can tile rectangles:

For other rectangles that these pentominoes tile, see Mike Reid's Rectifiable Polyomino Page.
Rodolfo Kurchan's online magazine Puzzle Fun studied the problem of tiling some rectangle with two different pentominoes, in Issue 19, and revisited the problem in Issue 21. The August 2010 issue of Erich Friedman's Math Magic broadened this problem to use two polyominoes of any size, not necessarily the same.
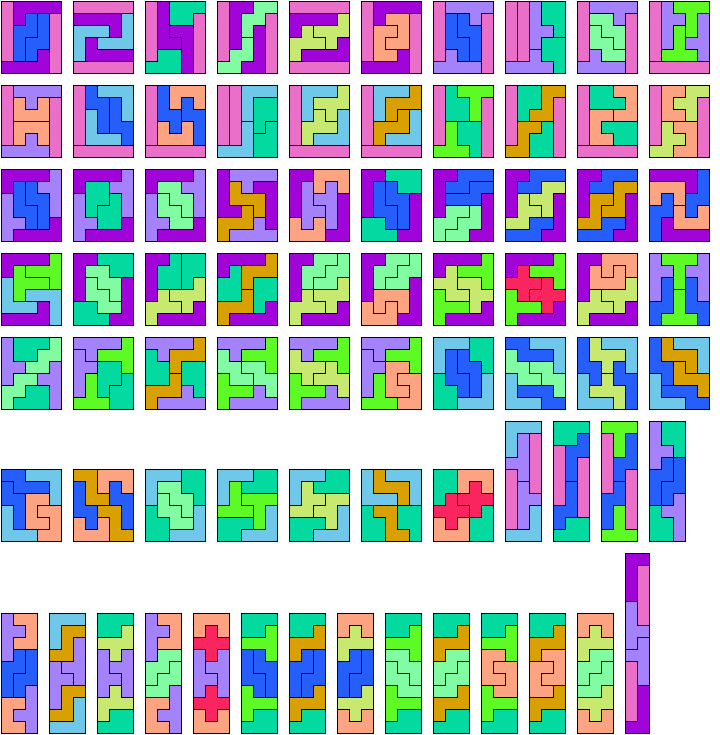
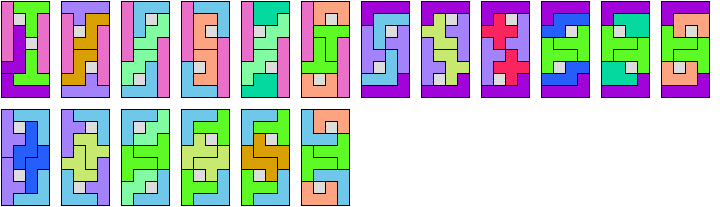
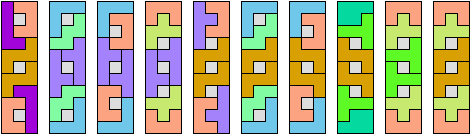
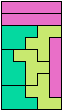
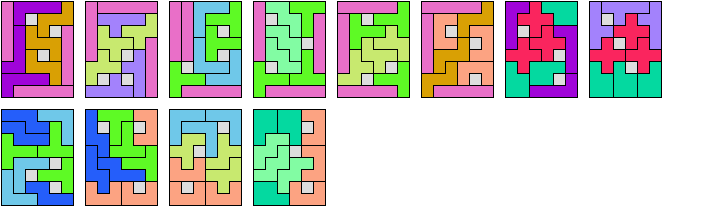
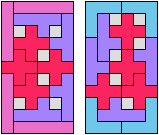
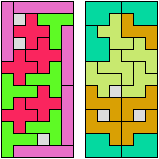
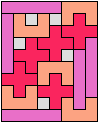
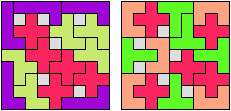
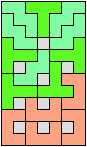
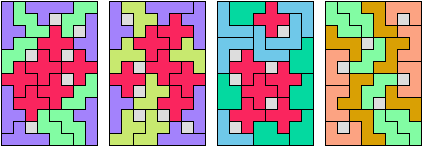
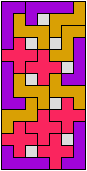
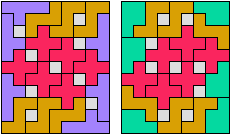
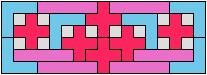
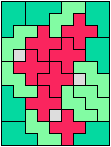
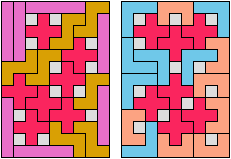
In Two-Pentomino Balanced Rectangles I study the related problem of tiling some rectangle with two pentominoes, using the same number of copies of each. Here I study the same problem, allowing one-cell holes in the rectangle. The holes must lie in the interior of the rectangle and must not touch one another.
Thanks to Jenard Cabilao for suggesting allowing holes in balanced pentomino rectangles.

| FIL | 30 | FUZ | 33 | IUY | 30 | LWZ | 63 | PVX | 96 |
| FIN | 63 | FVW | 63 | IUZ | 48 | LXY | 32 | PVY | 16 |
| FIP | 45 | FVX | 156 | IVW | 32 | LXZ | 98 | PVZ | 30 |
| FIT | 48 | FVY | 32 | IVX | 102 | LYZ | 30 | PWX | 108 |
| FIU | 30 | FVZ | 60 | IVY | 30 | NPT | 30 | PWY | 30 |
| FIV | 30 | FWX | × | IVZ | 30 | NPU | 15 | PWZ | 30 |
| FIW | 63 | FWY | 60 | IWX | 130 | NPV | 30 | PXY | 48 |
| FIX | 64 | FWZ | × | IWY | 30 | NPW | 60 | PXZ | 99 |
| FIY | 48 | FXY | 96 | IWZ | 63 | NPX | 64 | PYZ | 30 |
| FIZ | 63 | FXZ | × | IXY | 66 | NPY | 30 | TUV | 32 |
| FLN | 30 | FYZ | 60 | IXZ | 117 | NPZ | 30 | TUW | 84 |
| FLP | 30 | ILN | 30 | IYZ | 32 | NTU | 48 | TUX | 81 |
| FLT | 30 | ILP | 30 | LNP | 30 | NTV | 48 | TUY | 30 |
| FLU | 30 | ILT | 32 | LNT | 32 | NTW | 60 | TUZ | 64 |
| FLV | 16 | ILU | 30 | LNU | 30 | NTX | 126 | TVW | 32 |
| FLW | 30 | ILV | 30 | LNV | 15 | NTY | 30 | TVX | 130 |
| FLX | 81 | ILW | 30 | LNW | 30 | NTZ | 64 | TVY | 16 |
| FLY | 32 | ILX | 63 | LNX | 63 | NUV | 30 | TVZ | 32 |
| FLZ | 60 | ILY | 30 | LNY | 30 | NUW | 63 | TWX | 187 |
| FNP | 60 | ILZ | 48 | LNZ | 30 | NUX | 64 | TWY | 30 |
| FNT | 64 | INP | 30 | LPT | 32 | NUY | 30 | TWZ | 132 |
| FNU | 30 | INT | 30 | LPU | 16 | NUZ | 30 | TXY | 64 |
| FNV | 30 | INU | 30 | LPV | 15 | NVW | 30 | TXZ | × |
| FNW | × | INV | 30 | LPW | 30 | NVX | 64 | TYZ | 60 |
| FNX | × | INW | 63 | LPX | 48 | NVY | 32 | UVW | 35 |
| FNY | 60 | INX | 64 | LPY | 30 | NVZ | 30 | UVX | 117 |
| FNZ | × | INY | 30 | LPZ | 30 | NWX | × | UVY | 33 |
| FPT | 60 | INZ | 60 | LTU | 32 | NWY | 60 | UVZ | 33 |
| FPU | 15 | IPT | 30 | LTV | 30 | NWZ | × | UWX | 336 |
| FPV | 30 | IPU | 30 | LTW | 49 | NXY | 63 | UWY | 30 |
| FPW | 60 | IPV | 30 | LTX | 30 | NXZ | × | UWZ | 96 |
| FPX | 132 | IPW | 32 | LTY | 15 | NYZ | 60 | UXY | 30 |
| FPY | 30 | IPX | 64 | LTZ | 63 | PTU | 30 | UXZ | 162 |
| FPZ | 78 | IPY | 30 | LUV | 16 | PTV | 30 | UYZ | 33 |
| FTU | 33 | IPZ | 30 | LUW | 30 | PTW | 30 | VWX | 132 |
| FTV | 32 | ITU | 32 | LUX | 63 | PTX | 60 | VWY | 33 |
| FTW | 120 | ITV | 48 | LUY | 30 | PTY | 30 | VWZ | 33 |
| FTX | × | ITW | 48 | LUZ | 33 | PTZ | 33 | VXY | 66 |
| FTY | 30 | ITX | 78 | LVW | 16 | PUV | 15 | VXZ | 132 |
| FTZ | × | ITY | 30 | LVX | 64 | PUW | 48 | VYZ | 30 |
| FUV | 48 | ITZ | 63 | LVY | 32 | PUX | 30 | WXY | 96 |
| FUW | 30 | IUV | 32 | LVZ | 16 | PUY | 15 | WXZ | × |
| FUX | 156 | IUW | 63 | LWX | 63 | PUZ | 30 | WYZ | 60 |
| FUY | 33 | IUX | 80 | LWY | 30 | PVW | 30 | XYZ | 99 |








Last revised 2022-05-22.