Pentomino Pair Full Oddities
A polyomino oddity
is a symmetrical figure formed by an odd number of copies of
a polyomino.
Symmetrical figures can also be formed with copies of two
different pentominoes.
Here are the smallest known full-symmetry oddities
for the 66 pairs of pentominoes.
Some were found by Helmut Postl.
See also
| | F | I | L | N | P | T | U | V | W | X | Y | Z |
|---|
| F | * | 13 | 13 | 17 | 9 | 9 | 17 | 17 | 9 | 5 | 5 | 9 |
|---|
| I | 13 | * | 5 | 9 | 5 | 9 | 9 | 9 | 9 | 5 | 9 | 13 |
|---|
| L | 13 | 5 | * | 9 | 5 | 13 | 9 | 13 | 17 | 5 | 9 | 13 |
|---|
| N | 17 | 9 | 9 | * | 9 | 9 | 17 | 17 | 17 | 9 | 17 | 17 |
|---|
| P | 9 | 5 | 5 | 9 | * | 5 | 13 | 5 | 9 | 5 | 5 | 5 |
|---|
| T | 9 | 9 | 13 | 9 | 5 | * | 21 | 29 | 21 | 5 | 17 | 17 |
|---|
| U | 17 | 9 | 9 | 17 | 13 | 21 | * | 17 | 25 | 5 | 9 | 25 |
|---|
| V | 17 | 9 | 13 | 17 | 5 | 29 | 17 | * | 17 | 5 | 13 | 13 |
|---|
| W | 9 | 9 | 17 | 17 | 9 | 21 | 25 | 17 | * | 5 | 9 | 13 |
|---|
| X | 5 | 5 | 5 | 9 | 5 | 5 | 5 | 5 | 5 | * | 5 | 5 |
|---|
| Y | 5 | 9 | 9 | 17 | 5 | 17 | 9 | 13 | 9 | 5 | * | 5 |
|---|
| Z | 9 | 13 | 13 | 17 | 5 | 17 | 25 | 13 | 13 | 5 | 5 | * |
|---|
5 Tiles
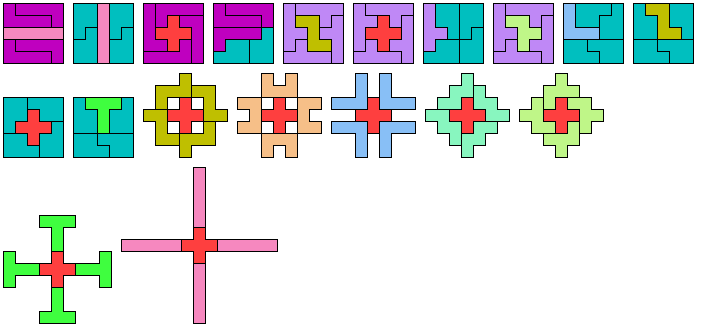
9 Tiles
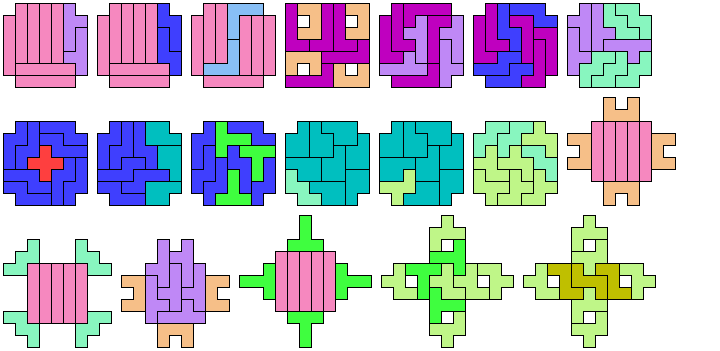
13 Tiles
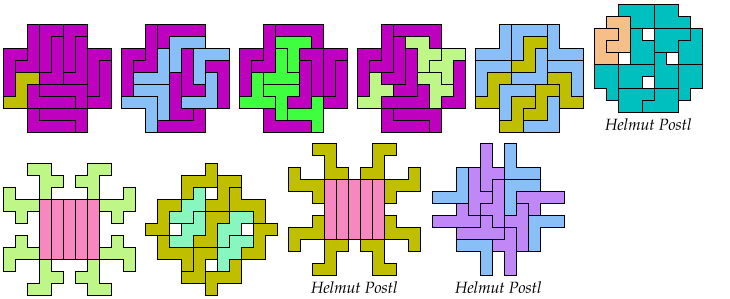
17 Tiles
21 Tiles
25 Tiles
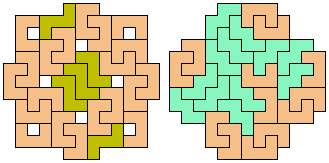
29 Tiles
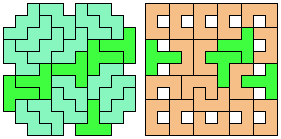
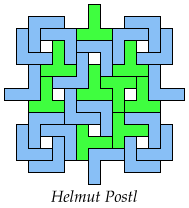Solutions shown above that are holeless are not shown here.
9 Tiles
13 Tiles
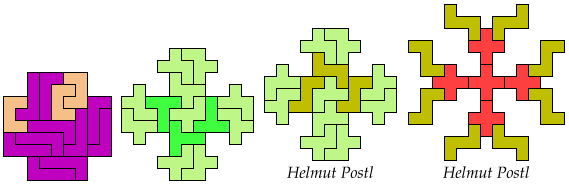
17 Tiles
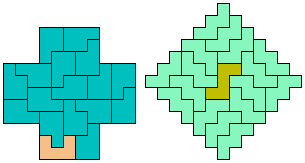
21 Tiles
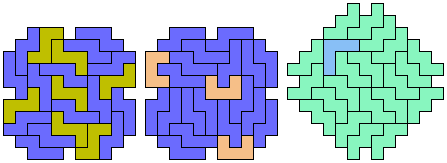
25 Tiles
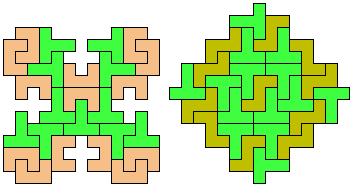
29 Tiles
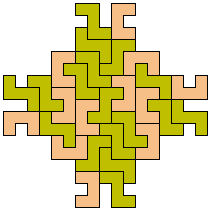
37 Tiles
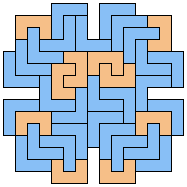
Last revised 2024-04-28.
Back to Polyform Oddities
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]