
At his website Atlantis, Dr. Karl Scherer introduced similar or scaled tetrads. These are arrangements of four geometrically similar figures in which each borders the other three. That is, they have the same shapes but not the same sizes. In general, scaled tetrads are easier to find that standard tetrads.
No rectangle can form a tetrad, with or without scaling. Here I show the smallest known scaled tetrads for non-rectangular polyominoes with from 3 to 6 cells. For each such polyomino I show a holeless tetrad if I know of one. Otherwise I show a tetrad with holes. If you find a holeless tetrad for a polyomino that was not known to have one, please write.

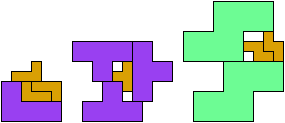
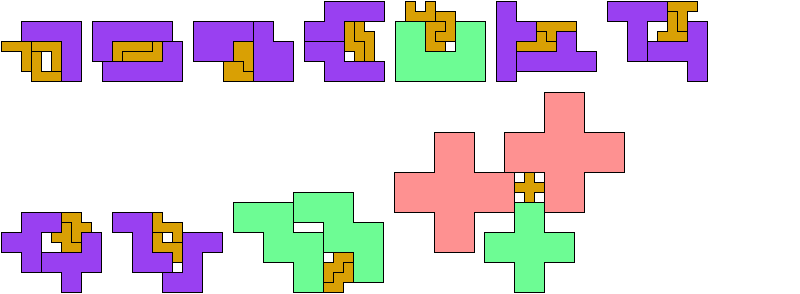
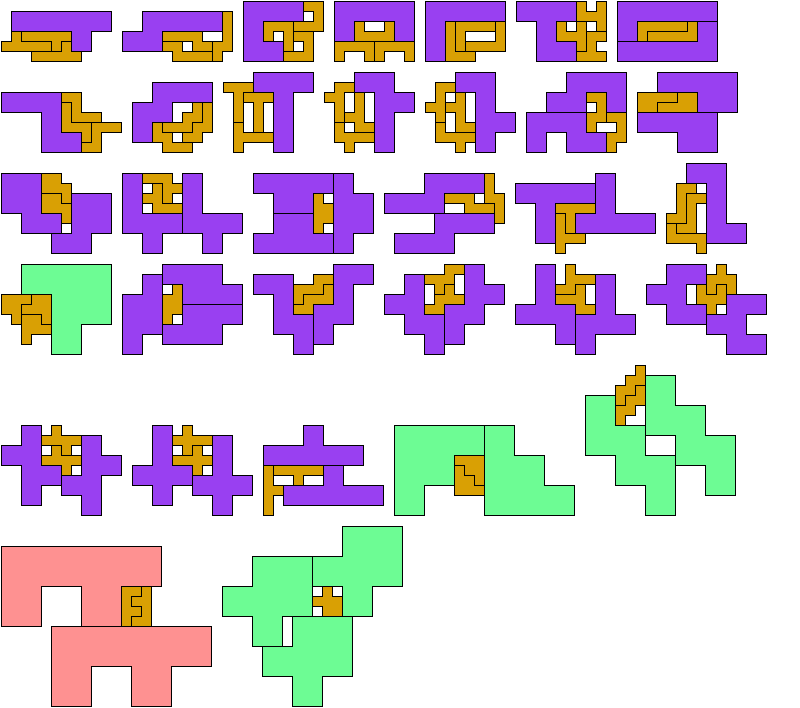
Last revised 2022-03-29.