Multiple Compatibility for Polyominoes

Introduction

A set of polyforms is compatible if there exists a figure that each of them can tile. Here are minimal figures that can be tiled by a given number of n-ominoes. Most are taken from Jorge Luis Mireles's defunct site Poly²ominoes. If you find a smaller solution or one that can be tiled by more n-ominoes, please write.

For arbitrary sets of three pentominoes, see Livio Zucca's Triple Pentominoes. For arbitrary sets of four pentominoes, see Quadruple Pentominoes.

For other polyforms, see Multiple Compatibility for Polyiamonds and Multiple Compatibility for Polyhexes.

Trominoes

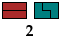
2 Trominoes

Tetrominoes

3 Tetrominoes

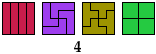
4 Tetrominoes

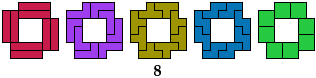
5 Tetrominoes

Pentominoes

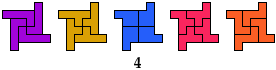
4 Pentominoes

5 Pentominoes

Solutions Using Other Pentominoes

5T, 5X

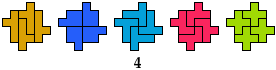
5V, 5W

5N

5U

5I

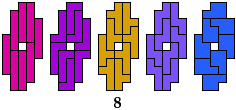
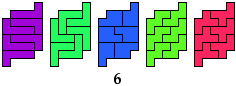
6 Pentominoes

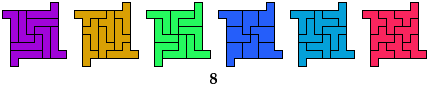
Rodolfo Kurchan

Solutions Using Other Pentominoes

5N, 5U, 5W

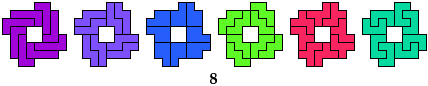
5I

5X

5Z

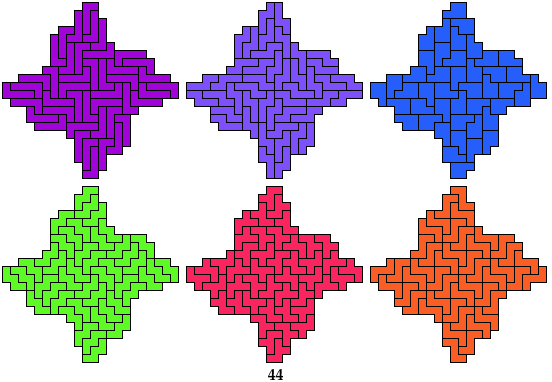
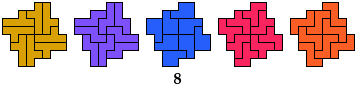
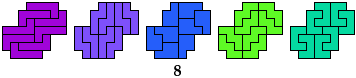
7 Pentominoes

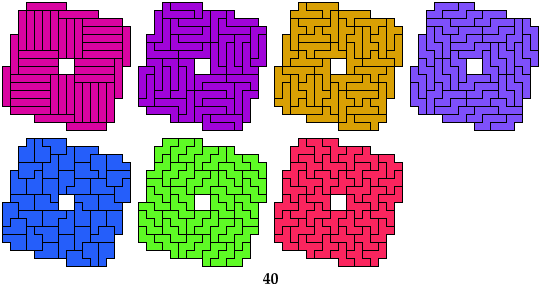
Alternate Solution

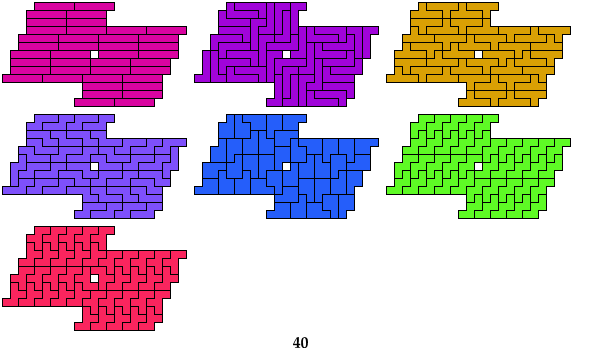
Holeless Solution

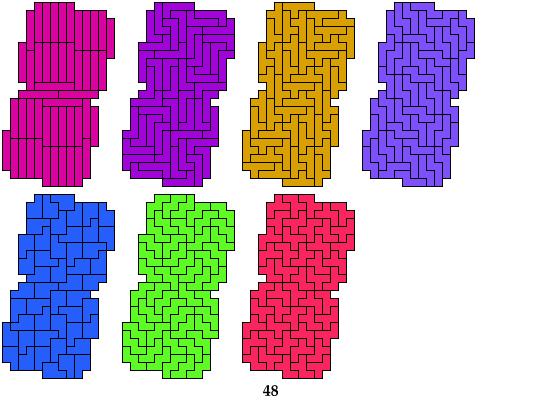
Historic Solution

This was the first solution found. It appeared in Puzzle Fun 6:

Mike Reid

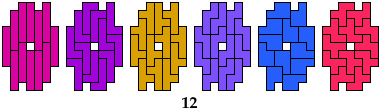
8 Pentominoes

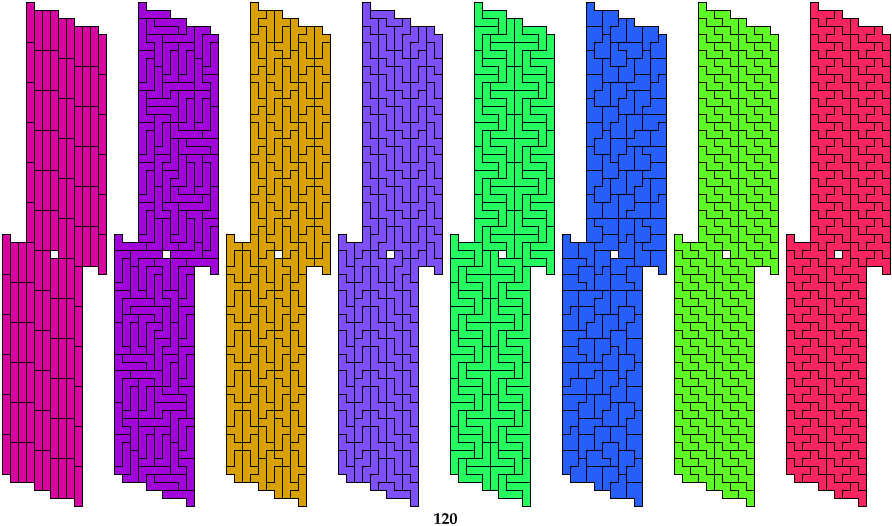
Hexominoes

6 Hexominoes

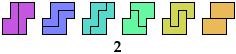
Solutions Using Other Hexominoes

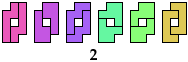
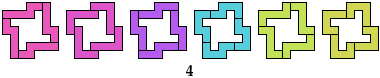
9 Hexominoes

Solutions Using Other Hexominoes

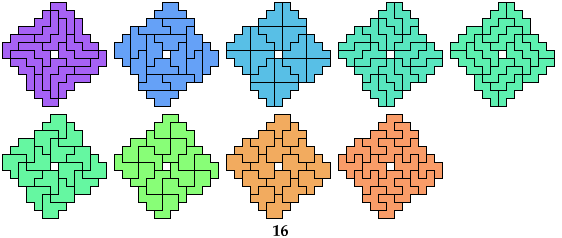
10 Hexominoes

Mike Reid

11 Hexominoes

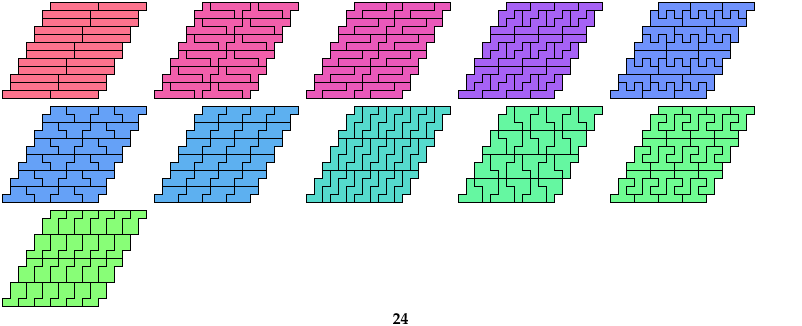
Mike Reid

12 Hexominoes

Mike Reid

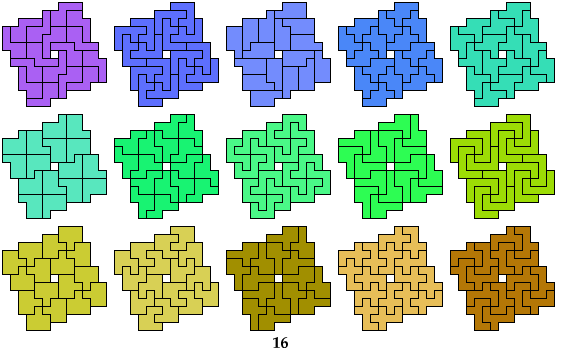
Heptominoes

9 Heptominoes

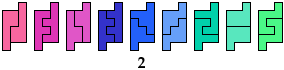
14 Heptominoes

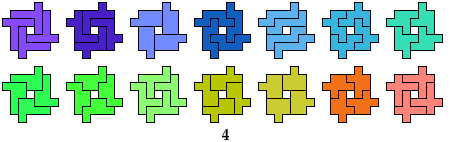
Robert Reid

15 Heptominoes

Last revised 2014-08-30.

Back to Multiple Compatibility < Polyform Compatibility < Polyform Curiosities

Col. George Sicherman [ HOME | MAIL ]