Covering a Rectangle with Copies of a Polyomino

Polyominoes with holes cannot tile the plane. For a polyomino with no holes that cannot tile the plane, we may ask what are the maximal rectangles and infinite strips that it can cover without overlapping, allowing the tiles to extend beyond the region's perimeter.

Every polyomino with 6 or fewer cells can tile the plane. For all holeless heptominoes and octominoes that do not tile the plane, and for selected larger polyominoes with these properties, the table below identifies the maximal rectangles and infinite strips that they can cover. Click on the dimensions of a rectangle to see a covering of it.

Thanks to Andris Cibulis for drawing my attention to polyomino covering problems.

Polyomino	Maximal Strips and Rectangles
Heptominoes (7 Cells)
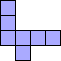
	4×ℕ, 5×8, 6×6
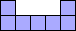
	4×ℕ, 6×19, 10×10
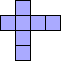
	4×ℕ, 6×6
Octominoes (8 Cells)
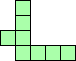
	4×ℕ, 5×9, 6×7
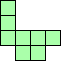
	4×ℕ, 5×28, 6×14, 8×10
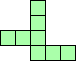
	4×ℕ, 5×10
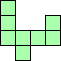
	8×ℕ, 9×22, 10×20, 11×12
	6×ℕ, 7×24, 8×16, 10×11
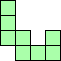
	3×ℕ, 4×18, 5×10, 7×8
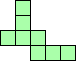
	4×ℕ, 5×10, 6×8
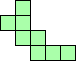
	4×ℕ, 5×22, 6×13, 7×9, 8×8
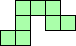
	8×ℕ, 10×10
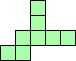
	4×ℕ, 5×10, 6×6
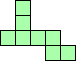
	6×ℕ, 7×26, 8×19, 9×12
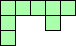
	4×ℕ, 5×14, 6×11, 7×10, 8×8
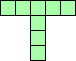
	4×ℕ
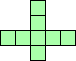
	4×ℕ
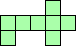
	4×ℕ, 5×18, 6×10, 8×8
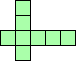
	4×ℕ, 5×8, 6×6
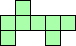
	8×ℕ, 10×10
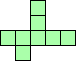
	4×ℕ, 5×10, 6×8
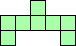
	3×ℕ, 4×13, 5×9, 6×8, 7×7
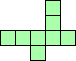
	4×ℕ, 5×17, 6×12, 7×8
Enneominoes (9 Cells)
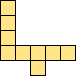
	2×ℕ, 3×50, 4×16, 5×7, 6×6
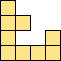
	2×ℕ, 3×6, 4×4,
	2×ℕ, 3×10, 4×4
	2×ℕ, 3×10, 4×5
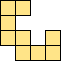
	1×ℕ, 2×12, 3×6
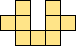
	2×ℕ, 3×6, 4×4
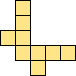
	2×ℕ, 3×12, 4×6
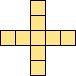
	2×ℕ, 3×3
Pentakaidecominoes (15 Cells)
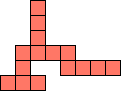
	1×40, 2×12, 3×6, 4×5
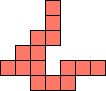
	1×25, 2×9, 3×5
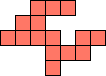
	1×40, 2×13, 3×8, 4×6
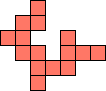
	1×22, 2×8, 4×4
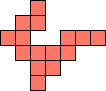
	1×32, 2×11, 3×6, 4×5
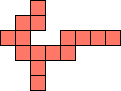
	1×22, 2×8, 4×4
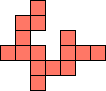
	1×22, 2×8, 3×5
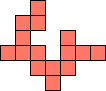
	1×26, 2×8, 4×4
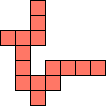
	1×36, 2×13, 3×6, 4×5
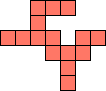
	1×26, 2×8, 3×4
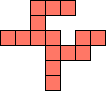
	1×28, 2×10, 3×4
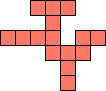
	1×34, 2×11, 3×8
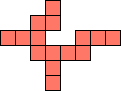
	1×21, 2×7, 3×5, 4×4
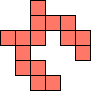
	1×26, 2×10, 3×4

Last revised 2020-11-28.