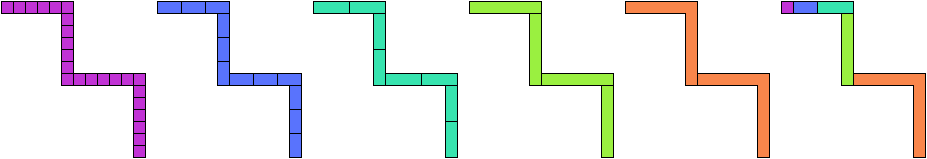Perfect Polyominoes

Introduction

A polyomino is a plane figure formed by joining equal squares edge to edge. A polyomino is perfect if it can be formed by joining one each of the smaller polyominoes that can tile it. The idea is due to Paul Salomon, and he and Justin Lanier were the first to investigate it. It was suggested by the perfect numbers of number theory. A perfect number is one that equals the sum of the smaller numbers that divide it evenly.

All known perfect numbers are even. Moreover, every even perfect number must be of the form 2^p(2^p+1 − 1), where the parenthesized expression is prime (a Mersenne prime). The first five perfect numbers are 6, 28, 496, 8128, 33550336. See the articles at Wikipedia and Mathworld.

Examples

The simplest perfect polyominoes are linear polyominoes whose lengths are perfect numbers. For example, 6 is a perfect number because its smaller divisors, 1, 2, and 3, add up to 6. Here is the corresponding perfect hexomino, showing the divisor tilings and the perfect tiling:

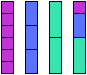
A straight polyomino is perfect if and only if its length is a perfect number.

The first nontrivial example of a perfect polyomino was given by Lanier:

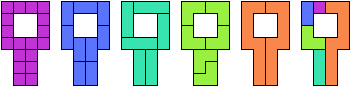
It has 18 cells, and its divisors have areas 1, 2, 3, 3, and 9, which sum to 18. Here are some perfect polyominoes with 18 cells and no holes:

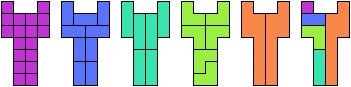
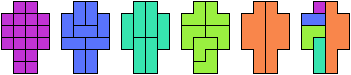
For a hexomino to be perfect, it must be tilable by the domino and exactly one of the two trominoes. Salomon and Lanier identify these hexominoes as perfect:

A polyomino may be perfect though it does not have a perfect number of cells. Of the 63600 12-ominoes, 346 are perfect. Here is an example:

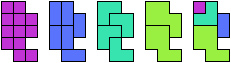
The divisors of 12 are 1, 2, 3, 4, and 6, which add up to 16. But this 12-omino cannot be tiled by any of the 5 tetrominoes.

Just as a polymino may have no divisor with a certain area that divides its own, it may also have several divisors with the same area:

This 45-omino is the smallest known perfect polyomino with an odd number of cells. Theoretically a 21-omino could have divisors with 1, 3, 3, 7, and 7 cells; but no 21-omino does.

Underlying Arithmetic

The areas of the tiles in a perfect polyomino tiling must evenly divide the area of the whole, and must add up to it. Thus if the perfect polymino has 12 cells, the areas of its divisors must be taken from the set {1,2,3,4,6}, allowing repetitions.

The nature of polyominoes imposes additional constraints.

The list of areas may not contain more copies of an area than exist polyominoes with that area. For example, there may not be more than two 3's, because there are only two different trominoes.
The number 1 must be in the set, because the monomino can tile every polyomino.
Other constraints follow from how some tiles can tile other tiles. Lanier gives this example: 1 + 3 + 4 + 4 = 12 is impossible because it lacks 2. The list contains two tetrominoes, at least one of which can be tiled by the domino!

Lanier provides this Existence Table of possible sets of divisor sizes for areas from 1 to 20. For areas from 21 to 45 see this page.

Generating Perfect Polyominoes

Salomon and Lanier give this general construction of a perfect polyomino whose area is a perfect number times a power of two:

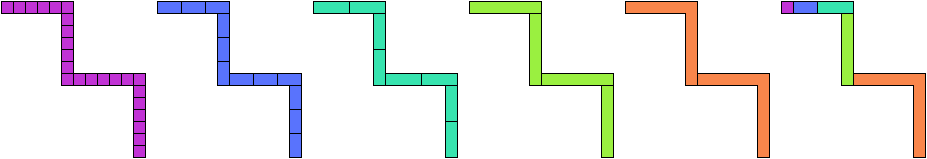
The construction can be duplicated arbitrarily many times to give a zigzag with 4, 8, 16, 32, … segments.

Other Polyforms

Any class of polyforms can have perfect members. This is especially true for plane-filling polyforms like polyiamonds, polyhexes, and polycairos. It is even truer for polycubes. Many 21-cell polycubes are perfect.

Last revised 2017-12-18.

Back to Polyform Tiling < Polyform Curiosities

Col. George Sicherman [ HOME | MAIL ]