Tetrominoes Challenge
Livio Zucca
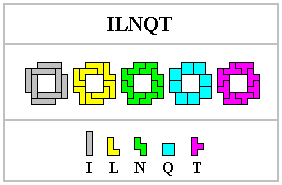
We are searching for the 25 shapes that can be covered by some tetrominoes AND NOT by the others. We'll give precedence to the solutions on the plane with the smallest surface. If you have better solutions, please write to George Sicherman HERE.
| ILNQ | ILNT | ILQT | INQT | LNQT |
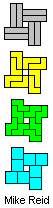 |
 |
 |
 |
 |
| ILN | ILQ | ILT | INQ | INT |
 |
 |
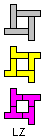 |
 |
 |
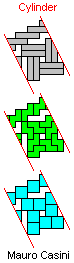
| IQT | LNQ | LNT | LQT | NQT |
 |
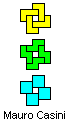 |
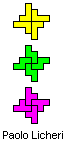 |
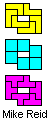 |
 |
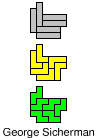
| IL | IN | IQ | IT | LN |
 |
 |
 |
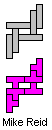 |
 |
| LQ | LT | NQ | NT | QT |
 |
 |
 |
 |
 |
Note by George Sicherman:
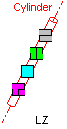
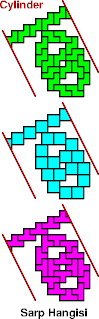
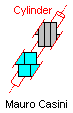
Mauro Casini originally found this reëntrant solution for NQT:
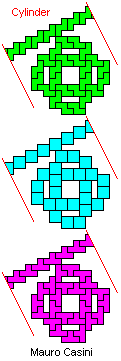
It uses Livio Zucca's original 24-tile solution to LNQT. In 2019, Sarp Hangisi improved this solution by replacing the 24-tile solution with my 16-tile solution.
Notice:
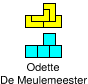
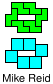
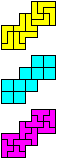
You can see here below, at left, the first IT solution with N= 10.
Afterwards, Mike Reid produced two improvements, one with N=8 and the
other with N=6. After few hours, I received the solutions of Helmut
Postl and Remmert Borst, with N=6 also.

The Mike's solutions are probably direct, on the contrary Helmut and Remmert derived their solutions from others.
For Helmut's solution we can write:
IT = ILT & INT
(I OR T) = (I OR L OR T) AND (I OR N OR T)
for Remmert's solution:
IT = ILQT & INT
(I OR T) = (I OR L OR Q OR T) AND (I OR N OR T)
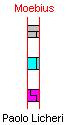
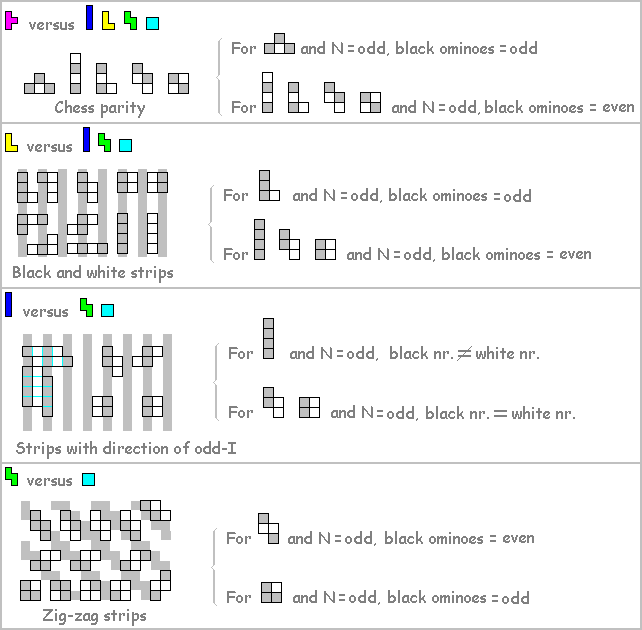
Proof that solutions with an odd number of tetrominoes cannot exist.
The demonstration is of Paolo Licheri.
George Sicherman
| ILT | IT | LQT | QT |
|---|---|---|---|

| 
| 
| 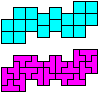
|
See also:
LINK:
Visit the wonderful
site of Jorge Luis Mireles (archived).
Zucca's
Challenge Problem for Polyiamonds
Zucca's
Challenge Problem for Tetrahexes
Zucca's
Challenge Problem for Extrominoes
_________________
It isn't trivial!
First edition: Dec. 24, 2003 — Last revision: Dec. 2, 2019


Hosted by Col. George Sicherman's Polyform Curiosities.



 Index
Index



