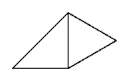

Its interior angles are 45°, 105°, 60°, and 150°. It was first studied by Dr. Karl Scherer.
Here I study the problem of determining the convex spectrum of the Scherer Quadrangle. The convex spectrum of a plane figure is the set of numbers n for which exactly n copies of the figure can be joined to form a convex shape. For a survey of convex spectra in general, and some surprising results, see Erich Friedman's Math Magic for April 1999.
You can download a page of printable Scherer Quadrangles here: { A4 } { letter size }
The tilings below are keyed by color:
 | Dr. Karl Scherer |
 | George Sicherman, 2013 |
 | Andrew Bayly, 2025 |
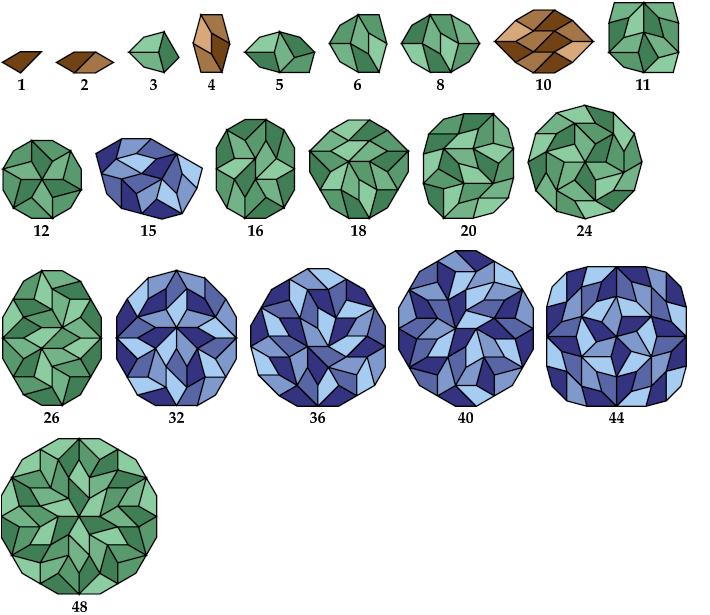
So the known convex spectrum of the Scherer Quadrangle is {1, 2, 3, 4, 5, 6, 8, 10, 11, 12, 15, 16, 18, 20, 24, 26, 32, 36, 40, 44, 48}. If you find any other values, please write!
Last revised 2025-09-05.