Polyomino and Polynar Tetrads

Introduction

A tetrad is a plane figure made of four congruent shapes, joined so that each shares a boundary with each. Here I show various minimal tetrads for polyominoes and polynars.

For similar or scaled tetrads, see Scaled Polyomino Tetrads.

Polyominoes

The smallest polyomino tetrads are made from octominoes:

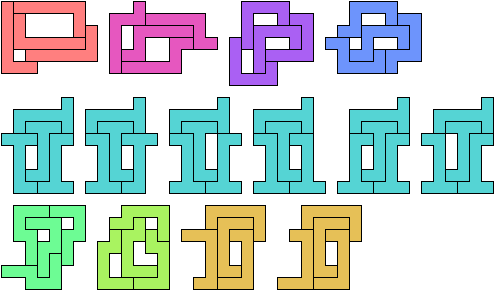
The fifth tetrad was reported by Olexandr Ravsky in 2005.

Symmetric Tiles

The smallest tetrad for a polyomino with mirror symmetry uses 13-ominoes:

The smallest tetrad for a polyomino with birotary symmetry also uses 13-ominoes:

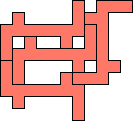
The smallest tetrads for polyominoes with birotary symmetry about an edge use 14-ominoes:

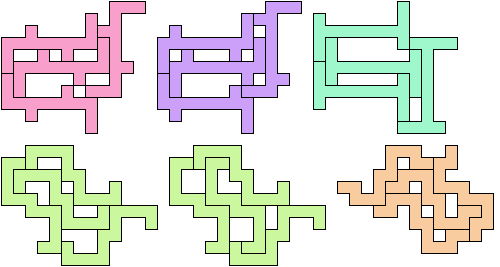
The smallest tetrads for polyominoes with mirror symmetry about an edge use 18-ominoes:

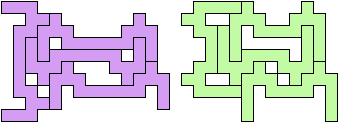
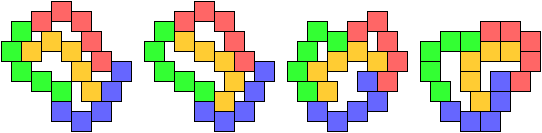
The smallest tetrads for polyominoes with birotary symmetry about a vertex also use 18-ominoes:

Juris Čerņenoks found the smallest tetrads for polyominoes with diagonal symmetry, which use 19-ominoes:

Restricted Motion

These octominoes form tetrads without being reflected:

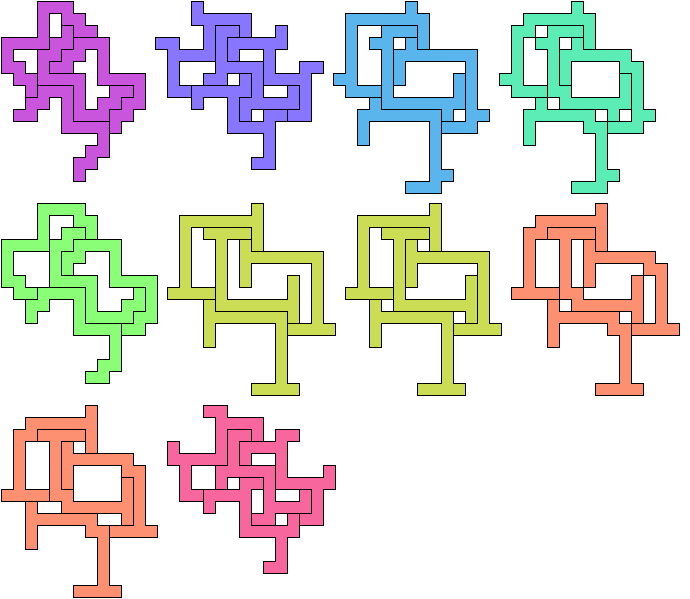
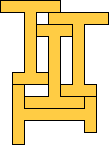
The smallest polyominoes that form tetrads without 90° rotation are 13-ominoes:

Holeless

The smallest holeless polyomino tetrad, discovered by Walter Trump, uses 11-ominoes:

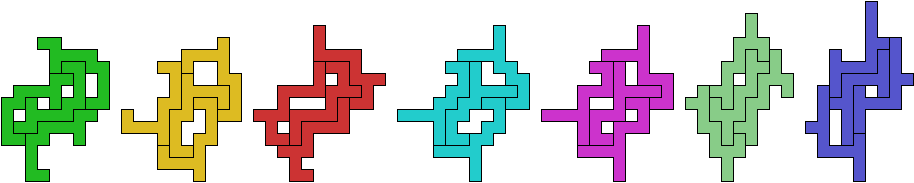
The smallest known holeless tetrad for a symmetric polyomino was found independently by Frank Rubin and Karl Scherer. It uses 34-ominoes:

Polynars

A polynar is a plane figure formed by joining equal squares along edges or half edges. The smallest polynar tetrads use pentanars:

Last revised 2020-01-14.

Back to Polyform Tetrads < Polyform Curiosities

Col. George Sicherman [ HOME | MAIL ]