Tetrahex-Pentahex Pair Hex-Convex Shapes
Introduction
A polyhex is said to be hex-convex
if every line joining the centers of two of its cells
lies in its interior.
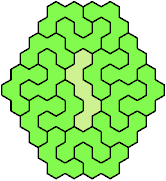
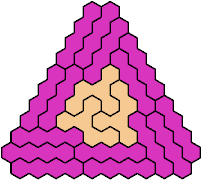
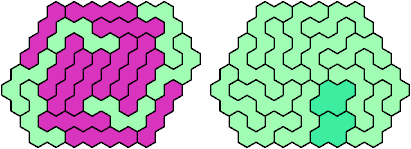
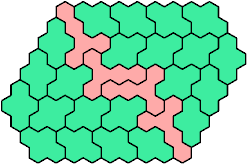
Here are the smallest known hex-convex polyhexes
that can be formed with copies of a tetrahex and a pentahex,
using at least one of each.
See also
If you find a smaller solution or solve an unsolved case, please write.
Nomenclature
Tetrahexes
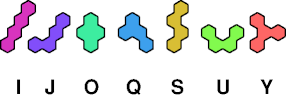
Pentahexes
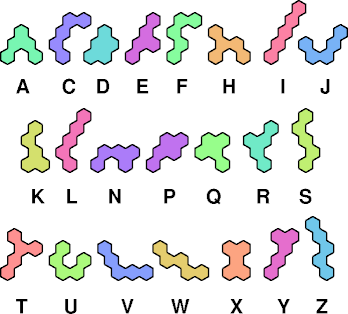
Table of Results
Each figure shows the number of cells in the corresponding tiling.
| | 5A | 5C | 5D | 5E | 5F | 5H | 5I | 5J | 5K | 5L | 5N | 5P | 5Q | 5R | 5S | 5T | 5U | 5V | 5W | 5X | 5Y | 5Z |
| 4I | 34 | 60 | 9 | 19 | 78 | 75 | 9 | 42 | 26 | 9 | 19 | 14 | 42 | 18 | 52 | 110 | 22 | 23 | 66 | 56 | 14 | 40 |
|---|
| 4J | 17 | 26 | 9 | 21 | 21 | 21 | 13 | 13 | 17 | 13 | 14 | 9 | 18 | 21 | 13 | 30 | 13 | 17 | 18 | 18 | 9 | 17 |
|---|
| 4O | 9 | 14 | 9 | 13 | 78 | 213 | 14 | 13 | 18 | 13 | 9 | 14 | 18 | 13 | 13 | 108 | 18 | 9 | — | 13 | 9 | 141 |
|---|
| 4Q | 9 | 17 | 9 | 13 | 13 | 21 | 17 | 9 | 21 | 13 | 9 | 9 | 17 | 18 | 21 | 29 | 13 | 18 | 18 | 17 | 13 | 18 |
|---|
| 4S | 18 | 18 | 39 | 24 | 58 | — | 54 | 22 | — | 18 | 18 | 14 | — | 70 | — | — | 18 | 30 | — | — | 24 | — |
|---|
| 4U | 17 | 18 | 13 | 9 | 18 | 26 | 31 | 18 | 18 | 19 | 13 | 14 | 18 | 26 | 69 | 60 | 13 | 27 | 114 | 13 | 14 | 28 |
|---|
| 4Y | 182 | — | 54 | — | — | — | — | 18 | — | 44 | 19 | 19 | — | — | — | — | 19 | — | — | — | 28 | — |
|---|
|
Navigation
[9 Cells]
[13 Cells]
[14 Cells]
[17 Cells]
[18 Cells]
[19 Cells]
[21 Cells]
[22 Cells]
[23 Cells]
[24 Cells]
[26 Cells]
[27 Cells]
[28 Cells]
[29 Cells]
[30 Cells]
[31 Cells]
[34 Cells]
[39 Cells]
[40 Cells]
[42 Cells]
[44 Cells]
[52 Cells]
[54 Cells]
[56 Cells]
[58 Cells]
[60 Cells]
[66 Cells]
[69 Cells]
[70 Cells]
[75 Cells]
[78 Cells]
[108 Cells]
[110 Cells]
[114 Cells]
[141 Cells]
[182 Cells]
[213 Cells]
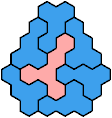
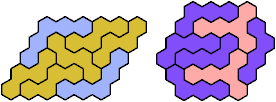
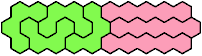
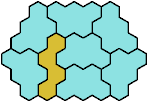
Solutions
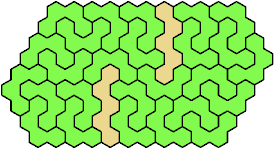
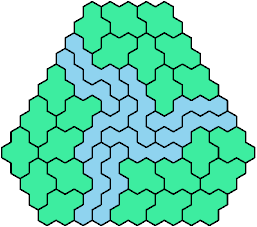
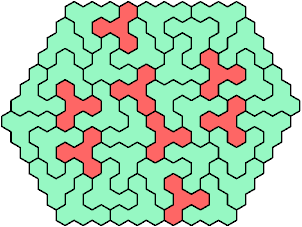
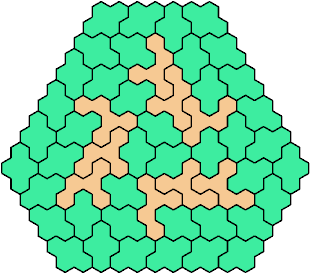
These minimal known solutions are not necessarily unique.


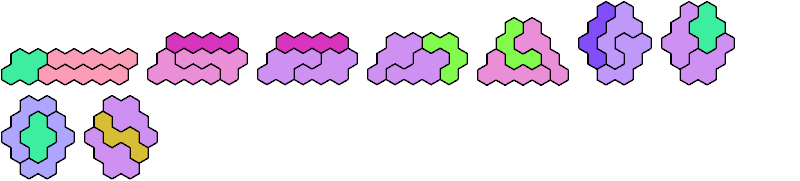




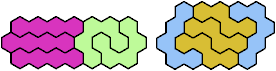
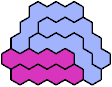
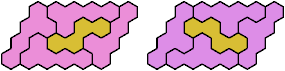
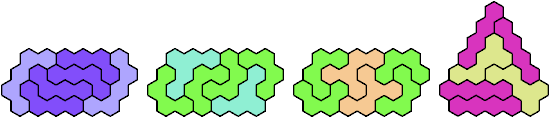

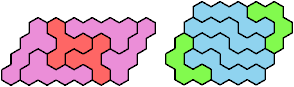


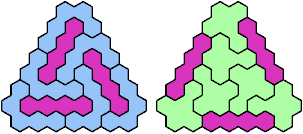


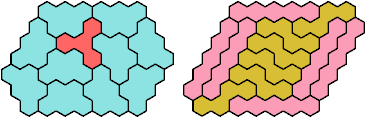

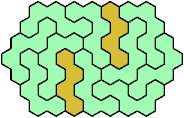
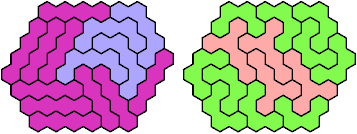



Last revised 2025-08-30.
Back to Polyhex Tiling
<
Polyform Tiling
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]







































