Tiling a Badge with Separated Copies of Three Pentahexes
Introduction
A polyhex
is a plane figure formed by joining equal regular hexagons
edge to edge.
A pentahex is a polyhex with 5 cells.
There are 22 pentahexes, not distinguishing reflections and rotations.
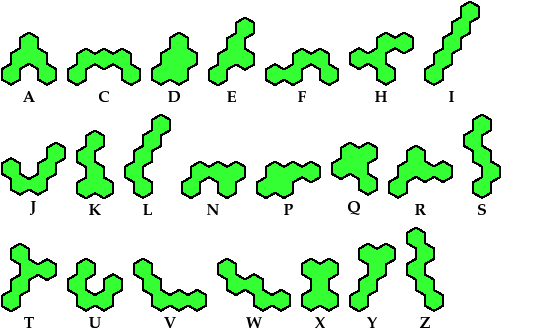
Let a polyhex badge be a polyhex whose cell centers form
a convex hexagon whose alternate sides have equal length.
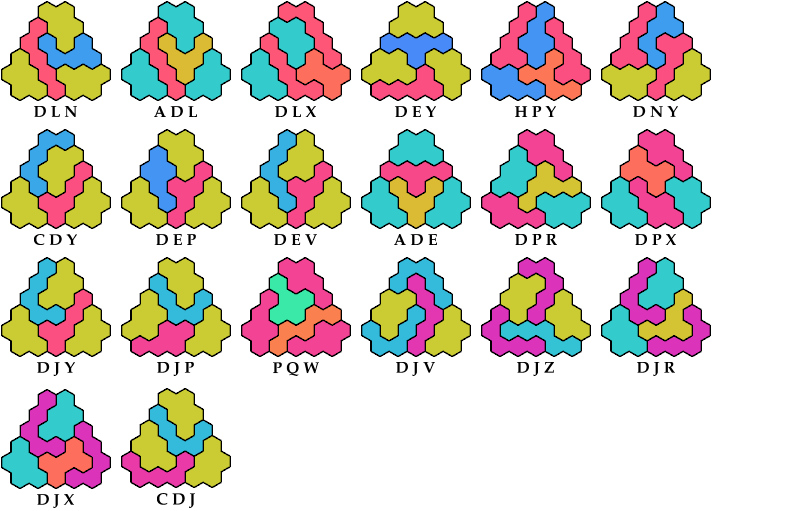
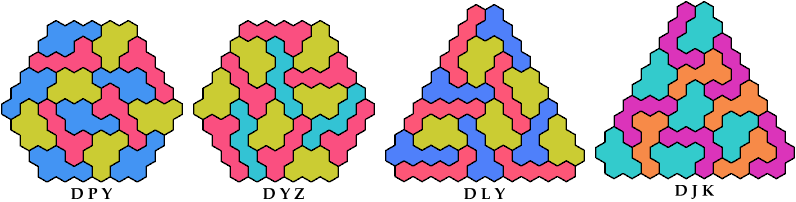
Here I study the problem of arranging copies of three given pentahexes
to form a badge, without letting two copies of a pentahex touch.
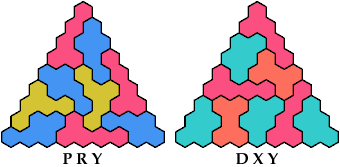
A triangular polyhex is an extreme form of a badge.
Many of the solutions below are triangular.
See the bottom of the page
for non-triangular variants.
Navigation
[3 Tiles]
[5 Tiles]
[9 Tiles]
[11 Tiles]
[12 Tiles]
[15 Tiles]
[18 Tiles]
[27 Tiles]
[38 Tiles]
[Non-Triangular Variants]


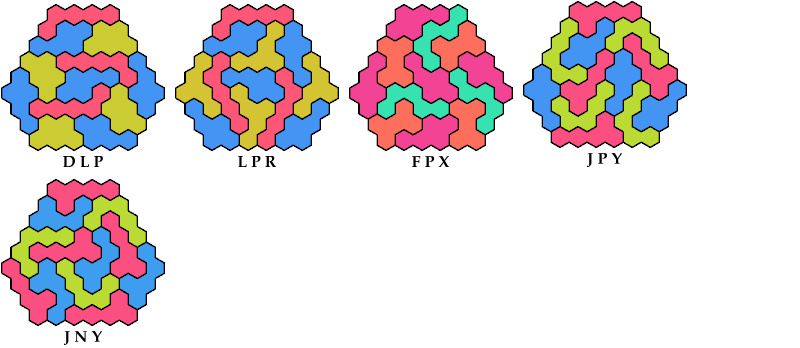


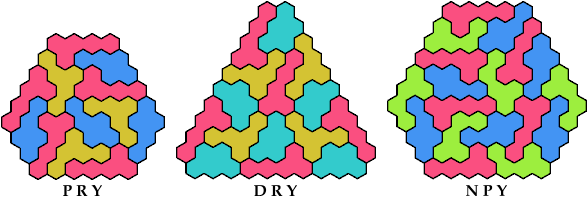
 These are non-triangular badges for some triples of pentahexes
whose minimal solution above is a triangular badge.
These are non-triangular badges for some triples of pentahexes
whose minimal solution above is a triangular badge.
Last revised 2025-06-12.
Back to Polyhex Tiling
<
Polyform Tiling
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]











