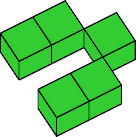
Prime Boxes for the Clip Pentakedge

A polykedge is a solid made of equal cubes joined face to face or edge to edge or both. A prime box for a polycube or polykedge is a rectangular prism, or box, that the polycube or polykedge can tile, and which cannot be dissected into smaller prime boxes. A polycube or polykedge can have at most finitely many prime boxes.

Here I list known prime boxes for the Clip Pentakedge in order of dimensions. The number of tilings shown is independent of rotations and reflections. For more information about box tilings by this tile, see this page by Torsten Sillke.

Additions and corrections are welcome!

Torsten Sillke has proved by coloring that this piece can tile only boxes whose volume is a multiple of 15. Only such boxes are shown here.

Tiles Dimensions Tilings Finder

24 3×4×10 6 Torsten Sillke

60 3×4×25 168 Torsten Sillke

36 3×6×10 68 Torsten Sillke

54 3×6×15 799 Torsten Sillke

42 3×7×10 10

63 3×7×15 2865

72 3×8×15

54 3×9×10 548

81 3×9×15

99 3×11×15

24 4×5×6 1 Torsten Sillke

84 4×7×15

96 4×8×15

108 4×9×15

132 4×11×15

66 5×6×11

84 5×6×14

102 5×6×17

84 5×7×12

210 5×7×30

72 5×8×9

90 5×9×10 Helmut Postl

150 5×10×15 Helmut Postl

Impossible

1×M×N

2×M×N

3×3×N Torsten Sillke

3×4×5

3×4×15 Torsten Sillke

3×5×N Torsten Sillke

4×4×N Torsten Sillke

4×5×N,
N ≢ 0 (mod 6)

5×5×N Torsten Sillke

5×6×6

5×6×7

5×6×9

5×6×10

5×6×13

5×7×9

5×7×15

5×7×18

5×7×21

5×7×27 Helmut Postl

5×9×9

5×9×11 Helmut Postl

5×9×12

5×9×13

5×9×14

5×9×15

5×9×17

Last revised 2022-04-13.

Back to Polycube Tiling < Polyform Tiling < Polyform Curiosities

Col. George Sicherman [ HOME | MAIL ]