

 | Pentacubes in a Box. Join copies of a pentacube to make a rectangular prism. |
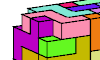 | Pentacubes in a Box Without Corners. Join copies of a pentacube to make a rectangular prism with its corner cells removed. |
 | Pentacubes in a Box With Four Edges Removed. Join copies of a pentacube to make a rectangular prism from which the cells along four parallel edges have been removed. |
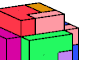 | Pentacubes in a Box With All Edges Removed. Join copies of a pentacube to make a rectangular prism from which the cells along the edges have been removed. |
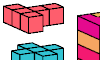 | Pentacube Pair Boxes. Join copies of two pentacubes, using one of each, to make a rectangular prism. |
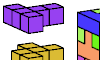 | Pentacube Pair Odd Boxes. Join copies of two pentacubes, using one of each, to make a rectangular prism with odd dimensions. |
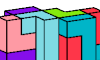
| Polycube Prisms. Join copies of a polycube to make a prism. |
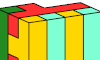
| Tiling L Shapes with a Pentacube. Join copies of a pentacube to make an L-shaped prism. |
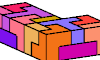
| L Shapes from Pentacube Pairs. Join copies of two pentacubes to make an L-shaped prism. |
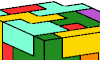
| L Shapes from the 29 Pentacubes. Join the 29 pentacubes to make an L-shaped prism. |
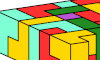
| Tiling a Triangular Prism Polycube with a Tetracube. Find a triangular prism polycube that can be tiled with copies of a given tetracube. |

| Tiling a Pyramid Prism Polycube with a Tetracube. Find a pyramid prism polycube that can be tiled with copies of a given tetracube. |
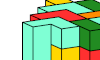
| Tiling a Diamond Prism Polycube with a Tetracube. Find a diamond prism polycube that can be tiled with copies of a given tetracube. |
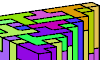
| Tiling a Triangular Prism Polycube with Two Pentacubes. Find a triangular prism polycube that can be tiled with two given pentacubes, using at least one of each. |

| Tiling a Pyramid Prism Polycube with Two Pentacubes. Find a pyramid prism polycube that can be tiled with two given pentacubes, using at least one of each. |

| Tiling a Diamond Prism Polycube with Two Pentacubes. Find a diamond prism polycube that can be tiled with two given pentacubes, using at least one of each. |
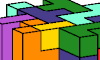
| Prisms with Square-Symmetric Bases from the 29 Pentacubes. Use all 29 pentacubes to form a prism whose base is a fully-symmetric 29-omino. |
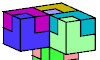 | Polycube Reptiles. Join copies of a polycube to make a larger copy of itself. |
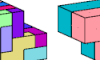 | Polycube Bireptiles. Join two copies of a polycube, then dissect the result into equal smaller copies of it. |
 | Proper Minimal Polycube Irreptiles. Join variously sized copies of a polycube to make a larger copy of itself, using fewer copies than would be needed if they were all the same size. |
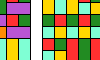 | Prime Boxes for the Clip Pentakedge. Identify the irreducible boxes that can be tiled by the Clip Pentakedge. |
 | 33 + 43 + 53 = 63. Dissect a cube of side 6 to make cubes of sides 3, 4, and 5. |
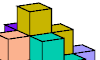 | Tiling a Solid Diamond Polycube With Right Tricubes. Dissect an octahedron-shaped polycube into L-shaped tricubes. |

| Symmetric Pentacube Triples. Join three different pentacubes to form a symmetric polycube. |

| Pentacube Pair Pyramids. Join copies of two pentacubes to make a pyramid. |
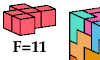
| Tiling a Cubic Polycube with Two Pentacubes. Join copies of two pentacubes to make a cube with side 5. |

| Tiling a Rhonic Polycube with Two Pentacubes. Join copies of two pentacubes to make a polycube shaped like a rhombic dodecahedron. |

| Tiling a Cuboctal Polycube with Two Pentacubes. Join copies of two pentacubes to make a polycube shaped like a cuboctahedron. |
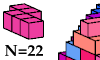
| Tiling a Heavy Cuboctal Polycube Shell with Pentacubes. Excise a heavy cuboctal polycube from a bigger one and tile the residue with copies of two or three pentacubes. |
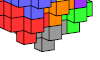
| Filling Space with the Pansymmetric Heptacube. Use the 3D analogue of an X pentomino to fill space. |
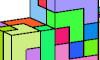
| Tiling a Scaled Pentacube with a Pentacube. Use a pentacube to tile various pentacubes scaled up by 2 or 3. |
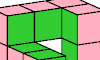
| Twisted Polycube Rings. Construct a re-entrant polycube with a twist in its loop. |

| Entangled Polycubes. Make a rectangular box out of polycubes that cannot be separated. |