Tiling a Heavy Cuboctal Shell Polycube with Pentacubes

Introduction

A pentacube is a solid made of 5 equal cubes joined face to face.

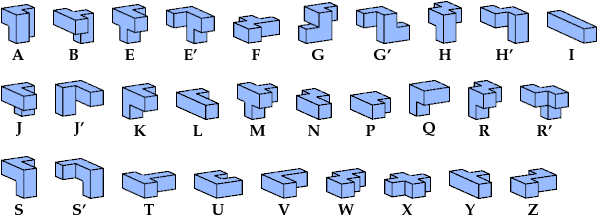
Mirror images are distinguished with a prime (′) mark.

A cuboctal polycube is a polycube whose cells form the shape of a cuboctahedron. A cuboctal polycube may be light or heavy depending on its structure at the edges of the cuboctahedron. In the picture below, the green polycube is light and the red polycube is heavy.

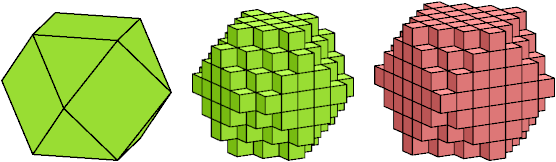
Bryce Herdt was the first to construct and analyze heavy cuboctal polycubes.

The heavy cuboctal polycubes shown below have 93 and 263 cells, respectively:

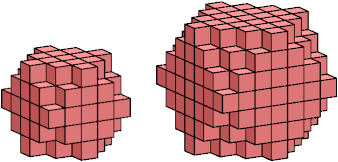
In March 2024, Edo Timmermans suggested excising the smaller of these polycubes from the larger, leaving a hollow shell with 170 cells, nd trying to tile the shell with 34 pentacubes.

If you solve an unsolved case, please write.

See also Tiling a Cuboctal Polycube with Two Pentacubes.

One Pentacube

No single pentacube can tile this shell.

Two Pentacubes

Two pentacubes can tile the shell, as shown below.

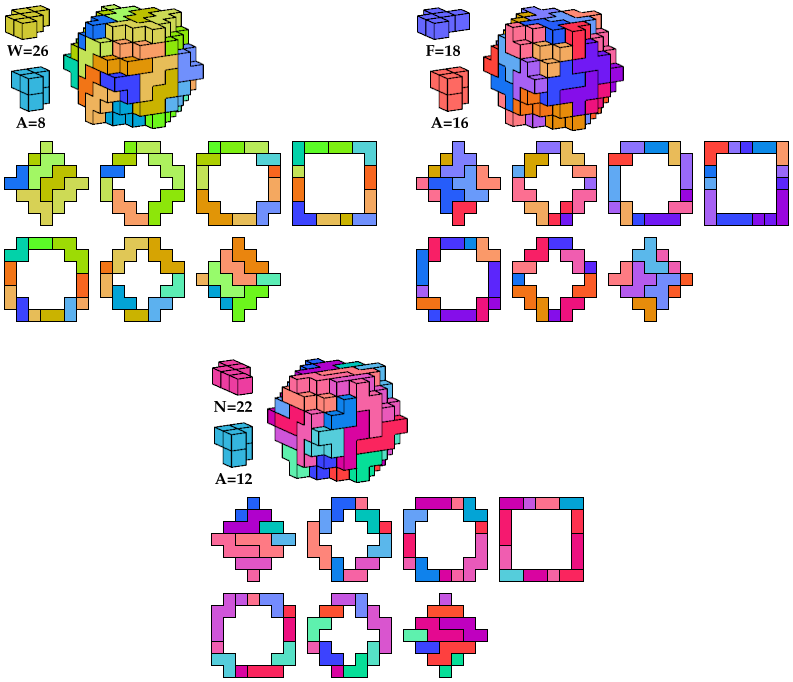
The bottom tiling has inverse (point) symmetry.

Three Pentacubes

Many sets of three pentacubes can tile this shell. To view a tiling, click on @ in the table below.

ABF @ AFZ @ ALR @ AQW @ BWX @ FHL @ HJN @ HVW @
ABL @ AGN @ ALU @ ARV @ EE′W @ FHV @ HJP @ HVX @
ABN @ AGP @ ALW @ ARW @ EFH′ @ FHX @ H′JP @ HVY @
ABP @ AGW @ ALY @ ARY @ EFW @ FRU @ H′JV @ HWX @
ABW @ AHL @ ANP @ ASW @ EH′L @ GHL @ H′JW @ HWY @
ABY @ AHN @ ANQ @ ATW @ EHN @ G′HL @ H′JY @ JNR′ @
AEF @ AHP @ ANR @ AUW @ EH′N @ GHP @ HLN @ JNW @
AEL @ AHV @ ANS @ AVW @ EHP @ G′HP @ HLP @ JPR′ @
AEN @ AHW @ ANT @ AWX @ EH′P @ GHV @ HLS @ JVW @
AEP @ AHX @ ANU @ AWY @ EH′V @ GNR @ HLV @ KWX @
AEW @ AHY @ ANV @ AWZ @ EHW @ GNW @ HLW @ LNR @
AFG @ AHZ @ ANW @ BFH @ EH′W @ GPR @ HNV @ LNW @
AFH @ AIN @ ANX @ BFR @ ELN @ G′PR @ HNX @ NRU @
AFJ @ AIP @ ANY @ BFW @ ELW @ GWX @ HPT @ NRV @
AFL @ AJL @ ANZ @ BHL @ ENR @ HH′I @ HPU @ NUW @
AFN @ AJN @ APQ @ BHN @ ENW @ HH′L @ HPV @ NVW @
AFP @ AJP @ APR @ BHP @ EPR @ HH′V @ HPX @ NWY @
AFR @ AJW @ APT @ BHW @ EPR′ @ HH′X @ HPY @ QWX @
AFT @ AKN @ APV @ BLW @ EPW @ HH′Y @ HRV @ RTX @
AFU @ AKP @ APW @ BNR @ EQW @ HH′Z @ HRX @ RVW @
AFV @ AKW @ APX @ BNW @ ERW @ HIP @ HSV @ RWX @
AFW @ ALN @ APY @ BPR @ ER′W @ HJL @ HTX @ TWX @
AFX @ ALP @ APZ @ BPW @ FG′H @ H′JL @ HUV @ VWY @
AFY @

Last revised 2024-03-06.

Back to Polycube Tiling < Polyform Tiling < Polyform Curiosities
Col. George Sicherman [ HOME | MAIL ]