Tiling L Shapes with a Pentacube

Introduction

A polycube is a solid made of equal cubes joined face to face, and a pentacube is a polycube with 5 cells. There are 29 pentacubes, distinguishing mirror images:

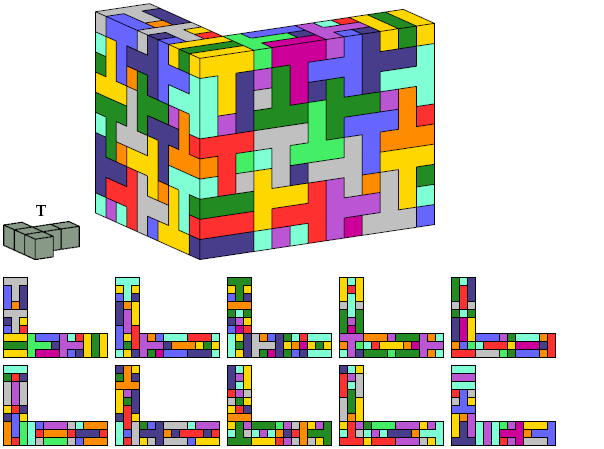
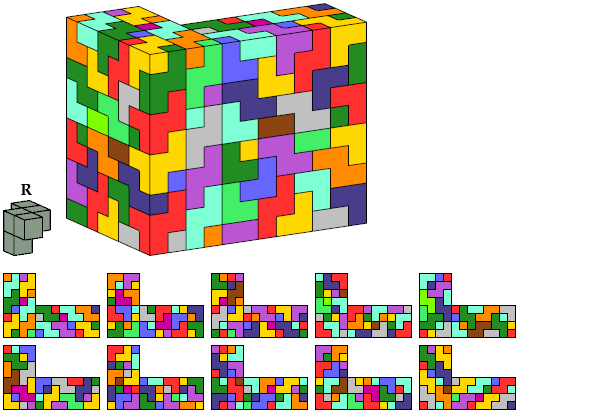
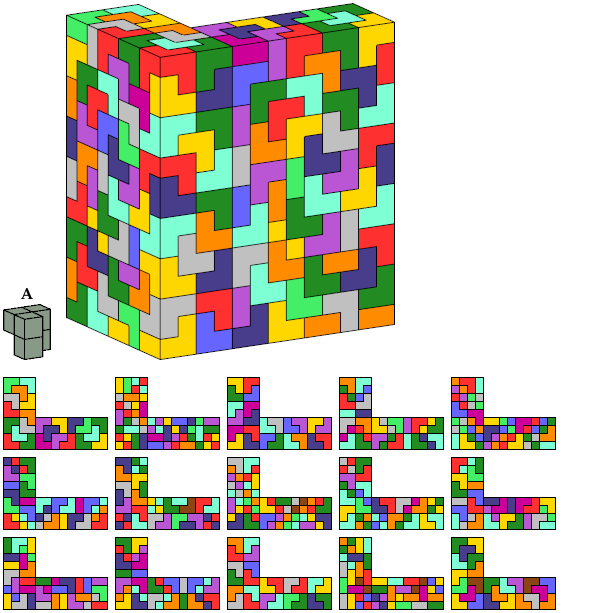
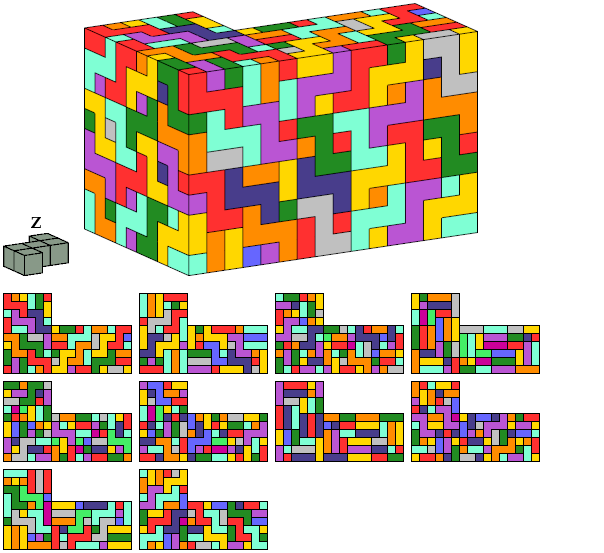
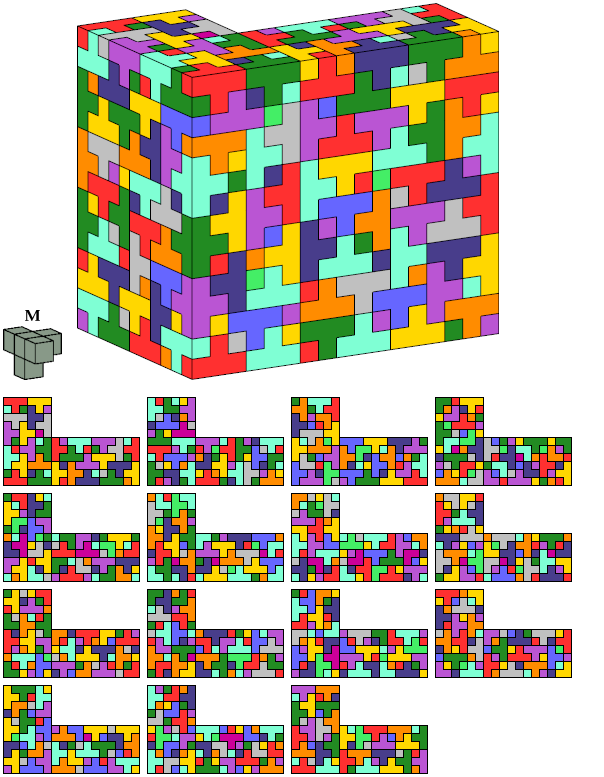
I define an L-shaped polycube as a polycube prism whose base is L-shaped; that is, it consists of a rectangle from one corner of which a smaller rectangle has been excised.

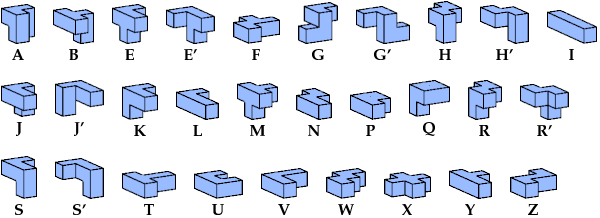
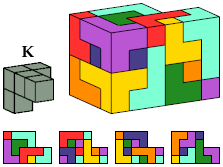
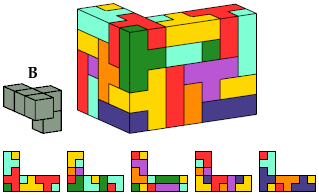
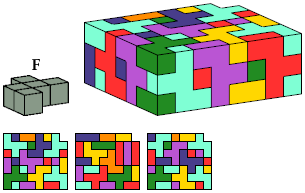
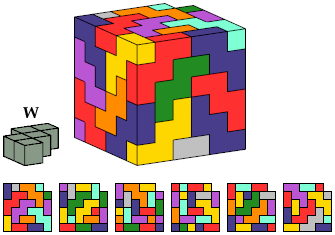
Here I show the smallest known L-shaped polycubes that can be tiled with a given pentacube. Chiral pairs of pentacubes are distinguished, and chiral pentacubes may not be reflected when used in these tilings.

If you find a smaller solution, please write.

See also L Shapes from Pentacube Pairs.

Tilings

The G and X pentacubes cannot tile any L-shaped polycube.

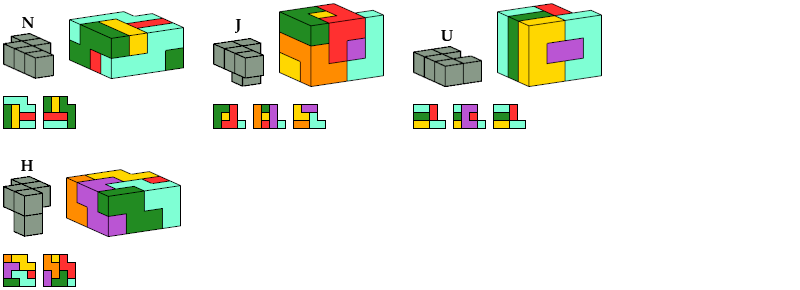
Each of the solutions shown for pentacubes T, R, A, Z, and M are formed by joining two rectangular box tilings. Smaller solutions may exist for these pentacubes.

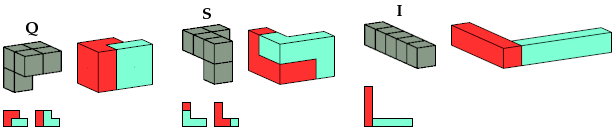
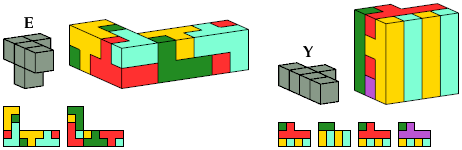
The solutions shown for pentacubes I, E, and B are formed by joining two rectangular box tilings. No smaller solutions exist for these pentacubes.

1 Tile

2 Tiles

6 Tiles

8 Tiles

16 Tiles

20 Tiles

33 Tiles

42 Tiles

120 Tiles

128 Tiles

216 Tiles

240 Tiles

396 Tiles

Last revised 2024-02-14.

Back to Polycube Tiling < Polyform Tiling < Polyform Curiosities
Col. George Sicherman [ HOME | MAIL ]