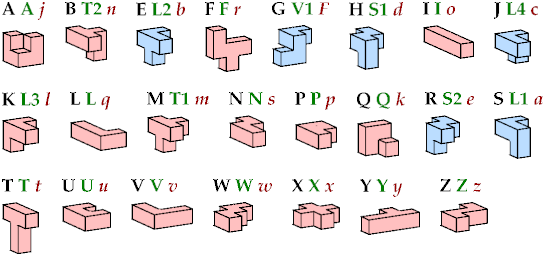

A rhonic polycube is a polycube whose cells form the shape of a rhombic dodecahedron.
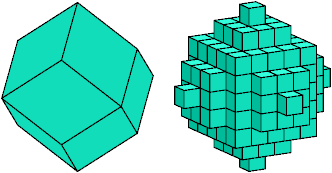
The smallest rhonic polycube whose volume is a multiple of 5 is the 5th rhonic polycube, shown above on the right. It has 185 cells, so it can be tiled with 37 pentacubes.
Here I show which pairs of pentacubes can tile this polycube, using at least one of each pentacube. A prime mark (′) after a letter denotes a mirror image. For example, S′ is the mirror image of S. To see a tiling, click on the corresponding entry in the table below. Missing entries indicate unsolved cases.
The B and Q pentacubes can each tile this polycube alone. To see such tilings, click on the corresponding index link in the table.
If you solve an unsolved case, please write.
See also Tiling a Cuboctal Polycube with Two Pentacubes and Pentacube Pair Pyramids.
| A | B | E | E′ | F | G | G′ | H | H′ | I | J | J′ | K | L | M | N | P | Q | R | R′ | S | S′ | T | U | V | W | X | Y | Z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | @ | @ | – | @ | – | × | – | – | × | × | – | – | @ | @ | × | × | × | – | – | × | × | × | |||||||
| B | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | @ | ||||||||
| E | @ | – | @ | @ | – | – | – | – | @ | – | – | – | – | – | @ | – | – | – | – | – | @ | – | – | – | – | – | |||
| F | – | – | × | – | – | – | × | – | – | @ | – | – | × | @ | – | – | × | – | – | ||||||||||
| G | @ | – | – | – | – | – | @ | @ | – | – | – | @ | @ | @ | – | – | – | – | – | × | – | – | – | ||||||
| H | – | – | – | – | – | – | – | – | – | @ | – | – | – | – | – | – | – | – | – | – | – | ||||||||
| I | – | – | × | × | × | – | @ | – | × | × | × | × | × | × | × | × | |||||||||||||
| J | @ | – | – | – | – | – | @ | @ | @ | – | – | – | – | – | – | – | @ | – | |||||||||||
| K | – | – | – | – | @ | @ | – | – | – | – | – | – | – | – | |||||||||||||||
| L | – | – | – | @ | – | × | – | × | – | – | × | × | × | ||||||||||||||||
| M | – | – | @ | – | – | – | – | – | – | × | – | – | |||||||||||||||||
| N | – | @ | – | – | – | – | – | – | – | – | – | ||||||||||||||||||
| P | @ | – | – | – | – | – | – | – | – | – | |||||||||||||||||||
| Q | @ | @ | @ | @ | @ | @ | @ | @ | @ | ||||||||||||||||||||
| R | @ | – | @ | – | @ | @ | – | – | – | – | |||||||||||||||||||
| S | × | × | × | – | × | × | × | × | |||||||||||||||||||||
| T | – | – | – | × | – | × | |||||||||||||||||||||||
| U | – | – | × | × | × | ||||||||||||||||||||||||
| V | – | – | – | – | |||||||||||||||||||||||||
| W | – | – | – | ||||||||||||||||||||||||||
| X | × | × | |||||||||||||||||||||||||||
| Y | × | ||||||||||||||||||||||||||||
| Z | |||||||||||||||||||||||||||||
Last revised 2024-03-18.