Multiple Compatibility for Pentacubes
Introduction
A set of polyforms is compatible
if there exists a figure that each of them can tile.
Here are minimal figures that can be tiled by a given number of
pentacubes.
If you find a smaller solution or one that can be tiled by more
pentacubes, please write.
For other polyforms,
see Multiple Compatibility
for Polyominoes,
Multiple Compatibility
for Polyiamonds,
and
Multiple Compatibility
for Polyhexes.
Nomenclature
I use these names for the 29 pentacubes:
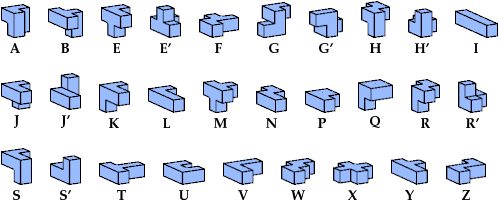
6 Pentacubes
2 Tiles



Mirror: B G′ J′ P Q R′
11 Pentacubes
4 Tiles
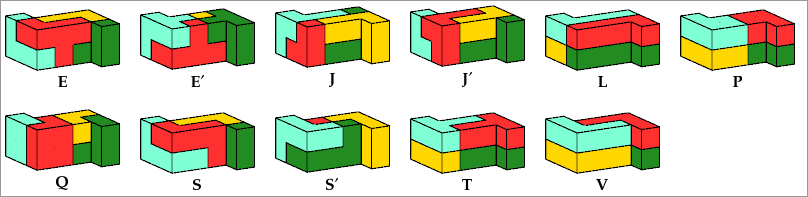
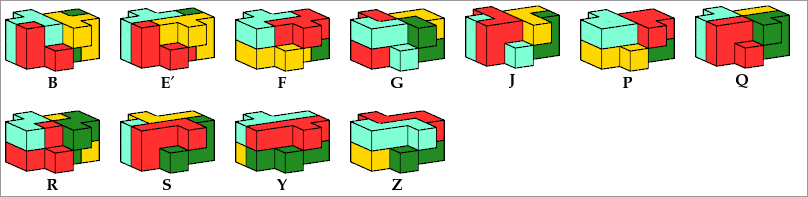
Mirror: B E F G′ J′ P Q R S Y Z
15 Pentacubes
6 Tiles
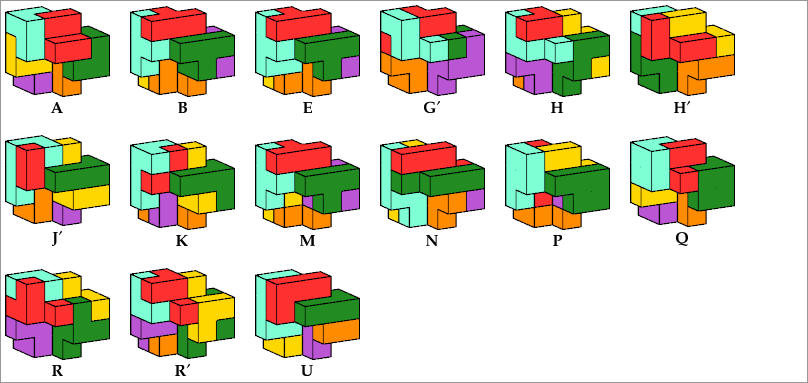
Mirror: A B E′ G H H′ J K M N P Q R R′ U
16 Pentacubes
8 Tiles
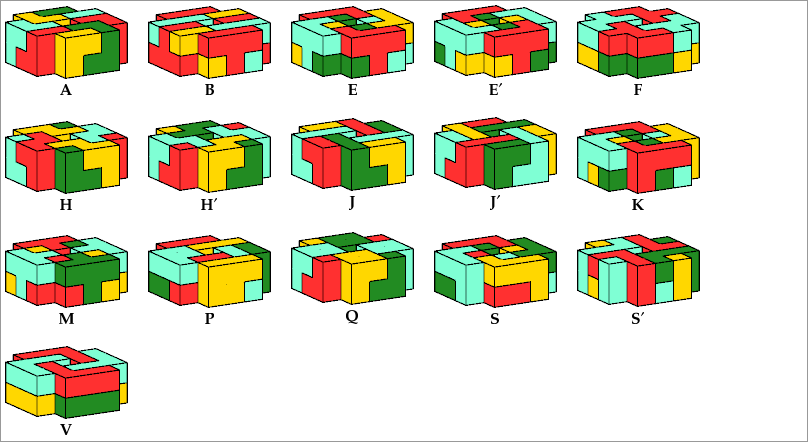
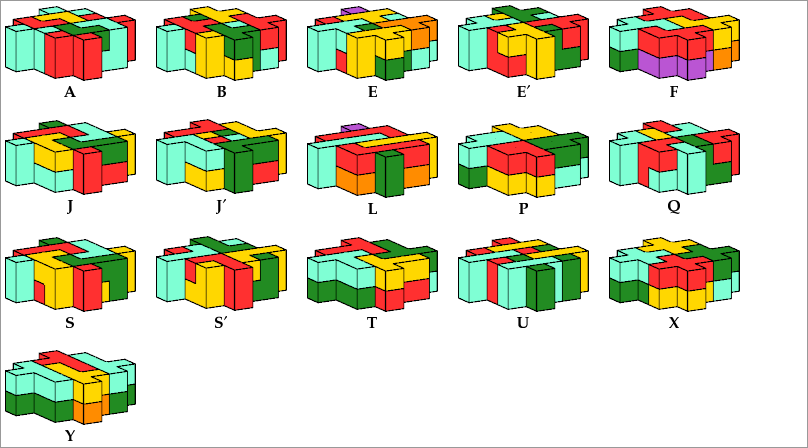
20 Pentacubes
16 Tiles
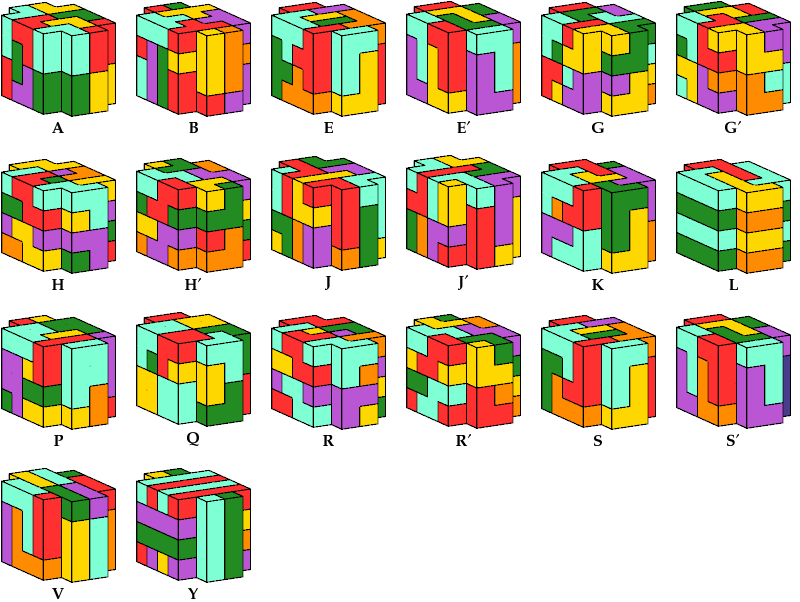
21 Pentacubes
24 Tiles

26 Pentacubes
240 Tiles
A 10×10×12 solid rectangular box
can be tiled by every pentacube but G,
G′, and X.
Those three pentacubes cannot tile any box.
Last revised 2023-08-20.
Back to Multiple Compatibility
< Polyform Compatibility
< Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]











