

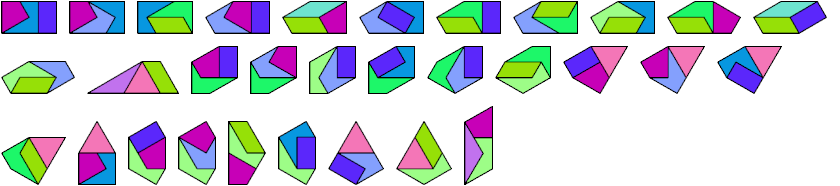
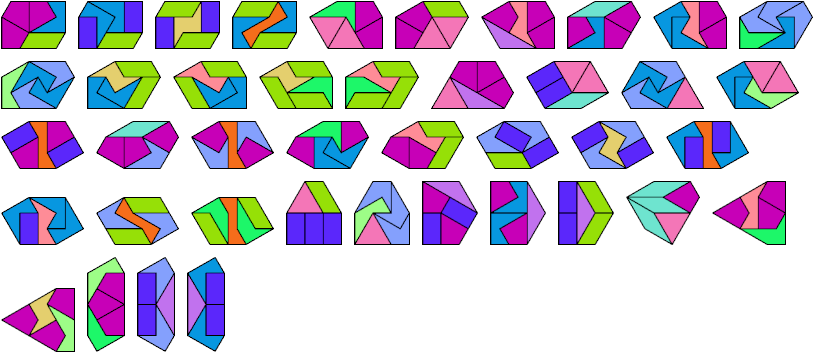
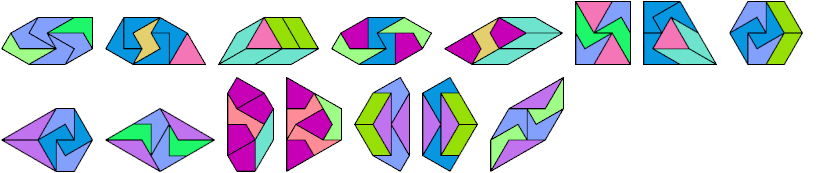
Below I show how to make a minimal convex figure using copies of three didrafters, at least one of each. These solutions are not necessarily unique, nor are their tilings. If you find a solution with fewer tiles, or solve an unsolved case, please write.
See also Convex Figures with Didrafter Pairs.
| 1-2-3 | 5 | 1-4-10 | 5 | 1-8-10 | 3 | 2-4-7 | 4 | 2-7-12 | 7 | 3-5-6 | 6 | 3-9-10 | 4 | 4-7-9 | 18 | 5-6-13 | 8 | 6-7-12 | 14 | 7-10-11 | × |
| 1-2-4 | 3 | 1-4-11 | × | 1-8-11 | × | 2-4-8 | 3 | 2-7-13 | 6 | 3-5-7 | 18 | 3-9-11 | × | 4-7-10 | 3 | 5-7-8 | 8 | 6-7-13 | 16 | 7-10-12 | × |
| 1-2-5 | 3 | 1-4-12 | × | 1-8-12 | 11 | 2-4-9 | 3 | 2-8-9 | 5 | 3-5-8 | 6 | 3-9-12 | × | 4-7-11 | × | 5-7-9 | 9 | 6-8-9 | 18 | 7-10-13 | × |
| 1-2-6 | 3 | 1-4-13 | × | 1-8-13 | 51 | 2-4-10 | 4 | 2-8-10 | 3 | 3-5-9 | 6 | 3-9-13 | × | 4-7-12 | × | 5-7-10 | × | 6-8-10 | 3 | 7-11-12 | × |
| 1-2-7 | 5 | 1-5-6 | 5 | 1-9-10 | 3 | 2-4-11 | 7 | 2-8-11 | 9 | 3-5-10 | 6 | 3-10-11 | × | 4-7-13 | × | 5-7-11 | × | 6-8-11 | 12 | 7-11-13 | × |
| 1-2-8 | 5 | 1-5-7 | 8 | 1-9-11 | × | 2-4-12 | 5 | 2-8-12 | 7 | 3-5-11 | × | 3-10-12 | × | 4-8-9 | 18 | 5-7-12 | × | 6-8-12 | 66 | 7-12-13 | × |
| 1-2-9 | 4 | 1-5-8 | 6 | 1-9-12 | × | 2-4-13 | 4 | 2-8-13 | 5 | 3-5-12 | × | 3-10-13 | × | 4-8-10 | 3 | 5-7-13 | 90 | 6-8-13 | 8 | 8-9-10 | 3 |
| 1-2-10 | 5 | 1-5-9 | 5 | 1-9-13 | × | 2-5-6 | 3 | 2-9-10 | 3 | 3-5-13 | 21 | 3-11-12 | × | 4-8-11 | 13 | 5-8-9 | 6 | 6-9-10 | 3 | 8-9-11 | × |
| 1-2-11 | 9 | 1-5-10 | × | 1-10-11 | × | 2-5-7 | 5 | 2-9-11 | 5 | 3-6-7 | 9 | 3-11-13 | × | 4-8-12 | × | 5-8-10 | 3 | 6-9-11 | 8 | 8-9-12 | × |
| 1-2-12 | 8 | 1-5-11 | × | 1-10-12 | × | 2-5-8 | 3 | 2-9-12 | 11 | 3-6-8 | 13 | 3-12-13 | × | 4-8-13 | × | 5-8-11 | × | 6-9-12 | × | 8-9-13 | × |
| 1-2-13 | 9 | 1-5-12 | 9 | 1-10-13 | × | 2-5-9 | 3 | 2-9-13 | 6 | 3-6-9 | 4 | 4-5-6 | 3 | 4-9-10 | 8 | 5-8-12 | 15 | 6-9-13 | 12 | 8-10-11 | 5 |
| 1-3-4 | 4 | 1-5-13 | 22 | 1-11-12 | × | 2-5-10 | 4 | 2-10-11 | 4 | 3-6-10 | 6 | 4-5-7 | 4 | 4-9-11 | × | 5-8-13 | 24 | 6-10-11 | 5 | 8-10-12 | 5 |
| 1-3-5 | 16 | 1-6-7 | 6 | 1-11-13 | × | 2-5-11 | 4 | 2-10-12 | 7 | 3-6-11 | 7 | 4-5-8 | 3 | 4-9-12 | × | 5-9-10 | 3 | 6-10-12 | 5 | 8-10-13 | 5 |
| 1-3-6 | 9 | 1-6-8 | 18 | 1-12-13 | × | 2-5-12 | 5 | 2-10-13 | 5 | 3-6-12 | 7 | 4-5-9 | 3 | 4-9-13 | × | 5-9-11 | × | 6-10-13 | 5 | 8-11-12 | × |
| 1-3-7 | 4 | 1-6-9 | 5 | 2-3-4 | 5 | 2-5-13 | 4 | 2-11-12 | × | 3-6-13 | 72 | 4-5-10 | 5 | 4-10-11 | 5 | 5-9-12 | 20 | 6-11-12 | × | 8-11-13 | × |
| 1-3-8 | 7 | 1-6-10 | 7 | 2-3-5 | 4 | 2-6-7 | 5 | 2-11-13 | 10 | 3-7-8 | 10 | 4-5-11 | 5 | 4-10-12 | × | 5-9-13 | 14 | 6-11-13 | × | 8-12-13 | × |
| 1-3-9 | × | 1-6-11 | 6 | 2-3-6 | 5 | 2-6-8 | 5 | 2-12-13 | 7 | 3-7-9 | 19 | 4-5-12 | 10 | 4-10-13 | 7 | 5-10-11 | × | 6-12-13 | × | 9-10-11 | 8 |
| 1-3-10 | 3 | 1-6-12 | 9 | 2-3-7 | 7 | 2-6-9 | 6 | 3-4-5 | 5 | 3-7-10 | 4 | 4-5-13 | 8 | 4-11-12 | × | 5-10-12 | 5 | 7-8-9 | × | 9-10-12 | × |
| 1-3-11 | × | 1-6-13 | 36 | 2-3-8 | 4 | 2-6-10 | 5 | 3-4-6 | 5 | 3-7-11 | × | 4-6-7 | 4 | 4-11-13 | × | 5-10-13 | 8 | 7-8-10 | 4 | 9-10-13 | 8 |
| 1-3-12 | × | 1-7-8 | 11 | 2-3-9 | 3 | 2-6-11 | 4 | 3-4-7 | 4 | 3-7-12 | × | 4-6-8 | 3 | 4-12-13 | × | 5-11-12 | × | 7-8-11 | × | 9-11-12 | × |
| 1-3-13 | × | 1-7-9 | 14 | 2-3-10 | 4 | 2-6-12 | 11 | 3-4-8 | 4 | 3-7-13 | × | 4-6-9 | 3 | 5-6-7 | 7 | 5-11-13 | × | 7-8-12 | × | 9-11-13 | × |
| 1-4-5 | 3 | 1-7-10 | 6 | 2-3-11 | 4 | 2-6-13 | 5 | 3-4-9 | 4 | 3-8-9 | 20 | 4-6-10 | 5 | 5-6-8 | 5 | 5-12-13 | 78 | 7-8-13 | × | 9-12-13 | × |
| 1-4-6 | 3 | 1-7-11 | × | 2-3-12 | 7 | 2-7-8 | 4 | 3-4-10 | 5 | 3-8-10 | 4 | 4-6-11 | 7 | 5-6-9 | 5 | 6-7-8 | 20 | 7-9-10 | 4 | 10-11-12 | × |
| 1-4-7 | 5 | 1-7-12 | × | 2-3-13 | 5 | 2-7-9 | 4 | 3-4-11 | 14 | 3-8-11 | × | 4-6-12 | 5 | 5-6-10 | 6 | 6-7-9 | 10 | 7-9-11 | × | 10-11-13 | × |
| 1-4-8 | 14 | 1-7-13 | × | 2-4-5 | 3 | 2-7-10 | 3 | 3-4-12 | 14 | 3-8-12 | 9 | 4-6-13 | 5 | 5-6-11 | 8 | 6-7-10 | 10 | 7-9-12 | × | 10-12-13 | × |
| 1-4-9 | × | 1-8-9 | 20 | 2-4-6 | 3 | 2-7-11 | 6 | 3-4-13 | 14 | 3-8-13 | 20 | 4-7-8 | 9 | 5-6-12 | 10 | 6-7-11 | 9 | 7-9-13 | × | 11-12-13 | × |
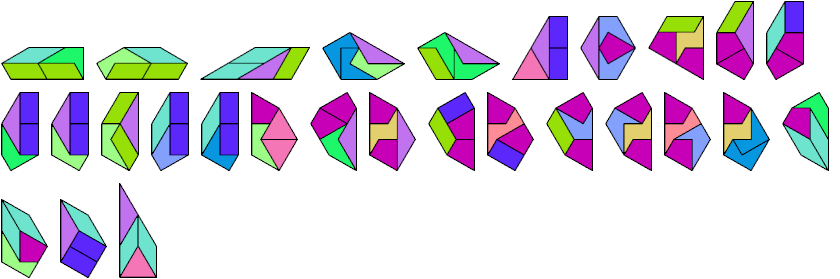
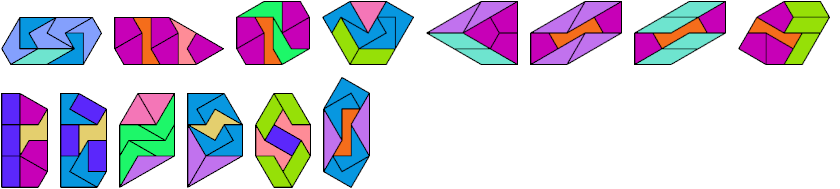
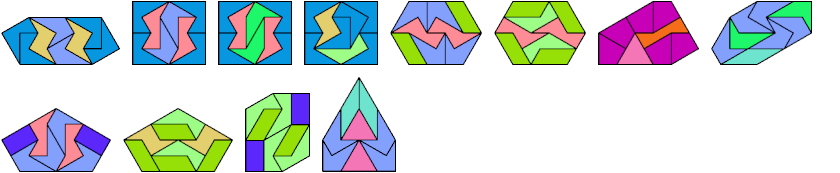
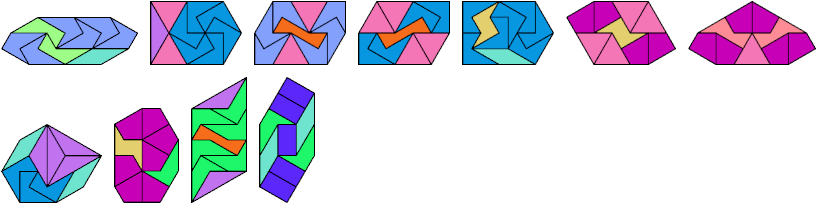

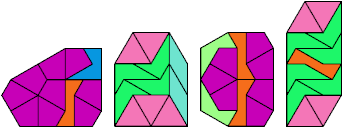


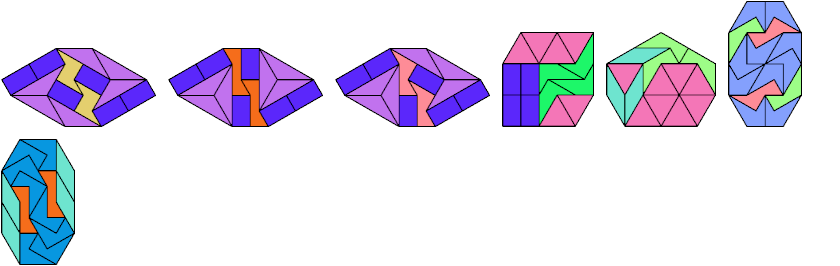

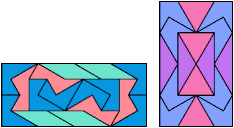

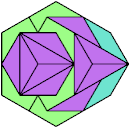
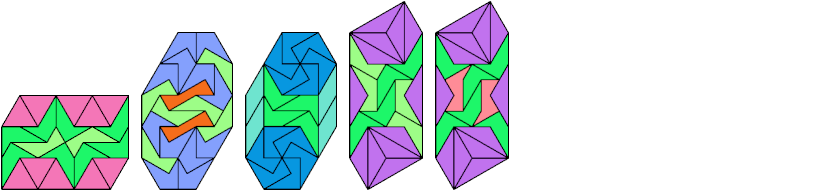









Last revised 2021-04-16.