Polydrafter and Polydrifter Tiling

	Polydrafter Irreptiling. Tile a polydrafter with smaller copies of itself, not necessarily equal.
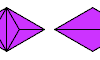	Polydrafter Bireptiles. Join two copies of a polydrafter, then dissect the result into equal smaller copies of it.
	The Didrafter Fish. Form a compact shape with the 13 proper and extended didrafters.
	Scaled Polydrafter Tetrads. Join four similar polydrafters so that each borders the other three.
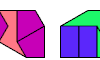	Convex Figures with Didrafter Pairs. Make a convex polydrafter with copies of two didrafters.
	Convex Figures with Didrafter Triplets. Make a convex polydrafter with copies of three didrafters.
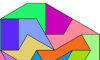	Convex Shapes from the 13 Didrafters. Make a convex polydrafter with the 13 didrafters.
	Rectangles Tiled with Three Didrafters. Make a rectangle with copies of three didrafters.
	Regular Hexagons Tiled with Three Didrafters. Make a regular hexagon with copies of three didrafters.
	Making a Rectangle from Different Didrafters. Make a rectangle out of up to eight distinct didrafters.
	Didrafters at Scales 1 and 5. Arrange a double set of the 13 didrafters to form copies of a didrafter at scales 1 and 5.
	Inflated Didrafters. Form a convex shape with the 13 didrafters after expanding some at integer scales or scales of an integer times √3.
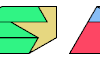	Convex Figures with Tridrafter Pairs. Make a convex shape with copies of two tridrafters.
	Galaxies from the 14 Tridrafters. Join the 14 proper tridrafters to make a shape with 6-rotary symmetry.
	Tiling a Scaled Didrifter with Distinct Didrifters. Arrange 25 of the 27 conforming didrifters to form a didrifter scaled up by a factor of 5.
	Stelo Twins and Triplets. Use Jacques Ferroul's Stelo pieces to make multiple copies of the same shape.