2 Tiles
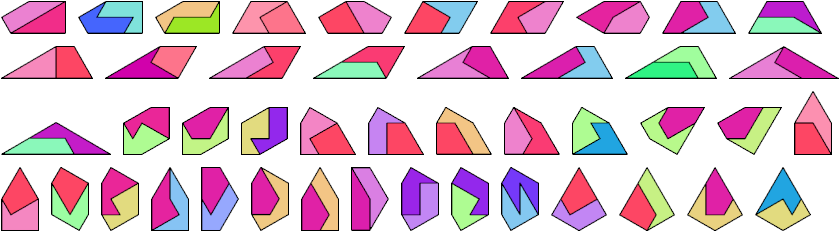
3 Tiles

4 Tiles
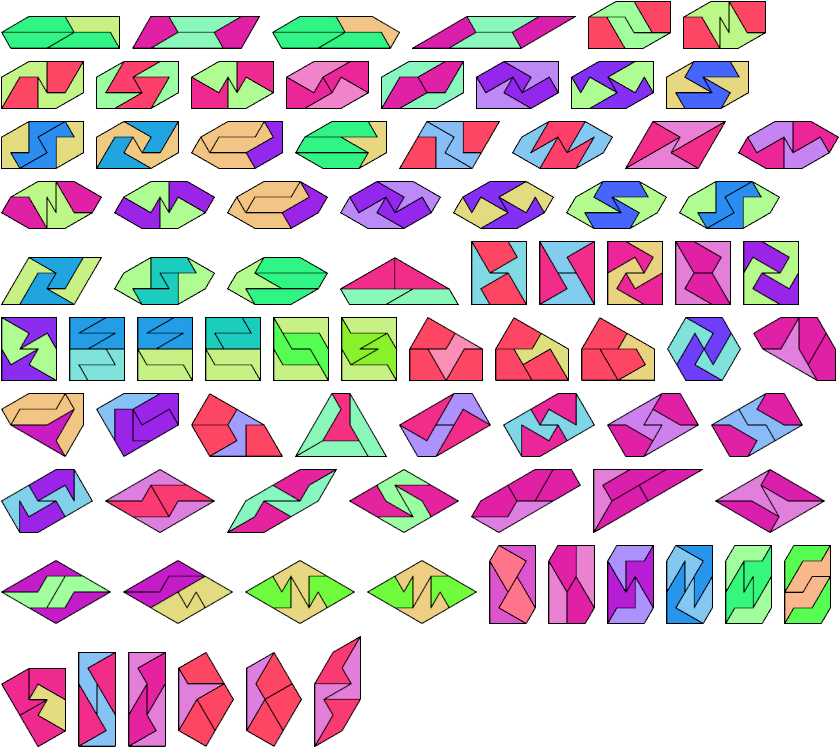
5 Tiles
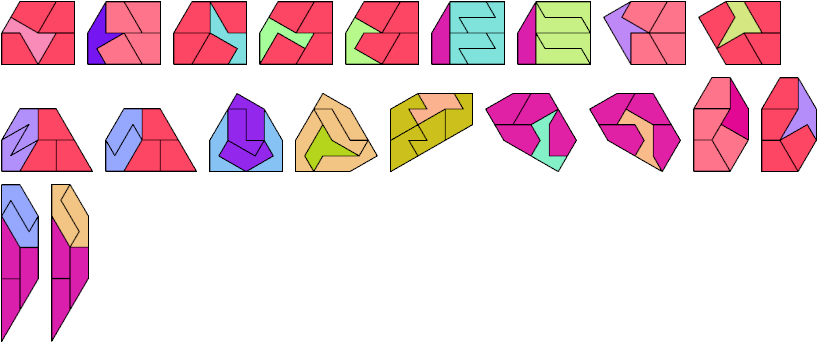
6 Tiles

7 Tiles

8 Tiles

9 Tiles
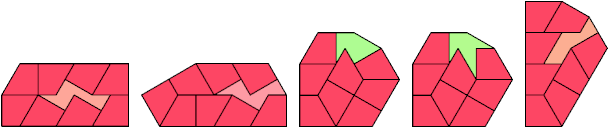
10 Tiles

11 Tiles
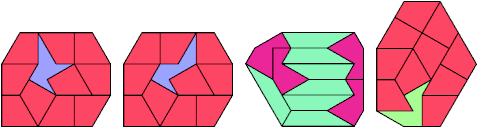
12 Tiles

14 Tiles
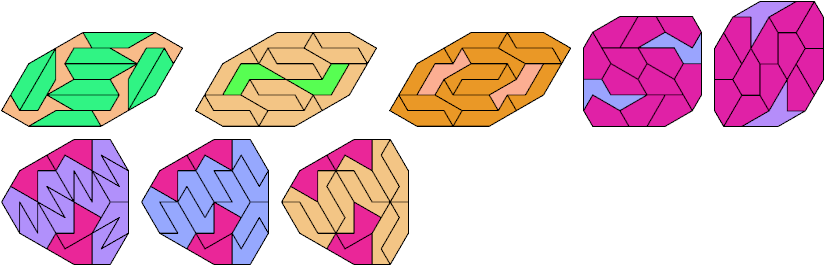
16 Tiles
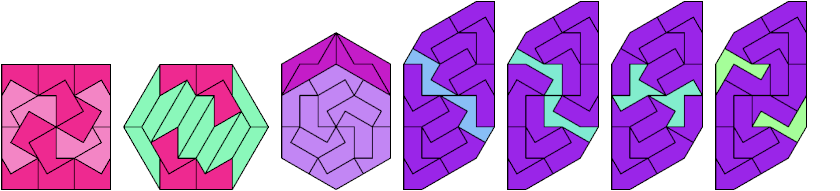
17 Tiles
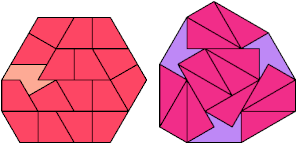
18 Tiles
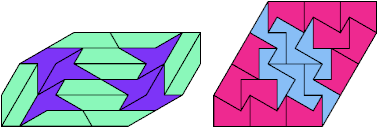
20 Tiles
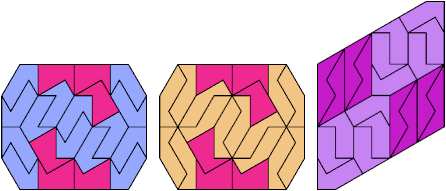
22 Tiles
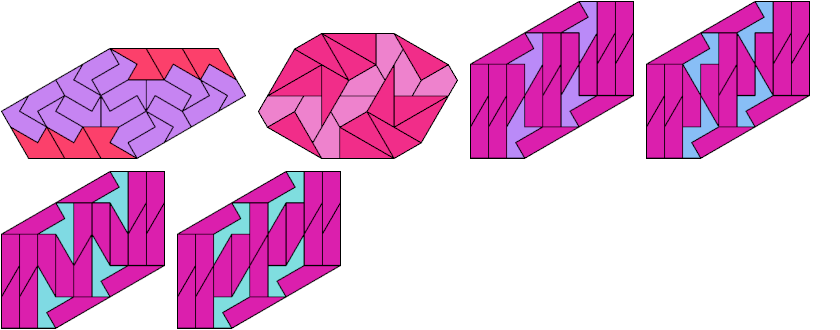
23 Tiles
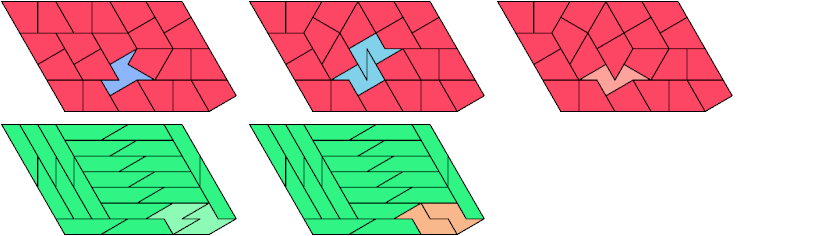
24 Tiles
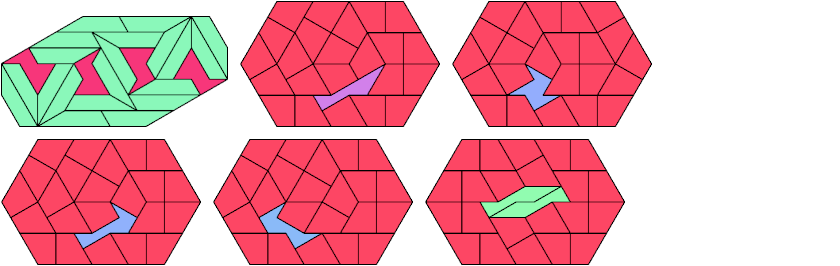
26 Tiles
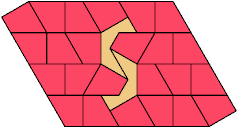
29 Tiles
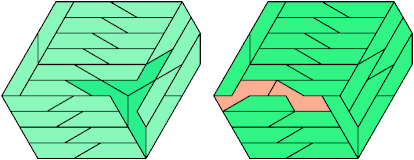
36 Tiles
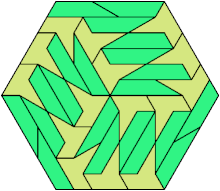
38 Tiles
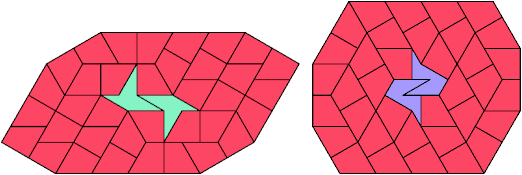
40 Tiles
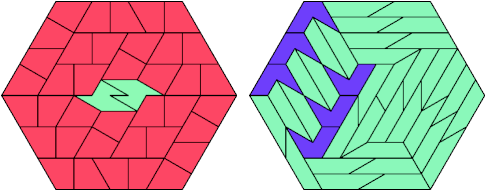
42 Tiles
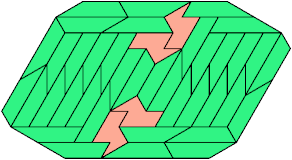
48 Tiles
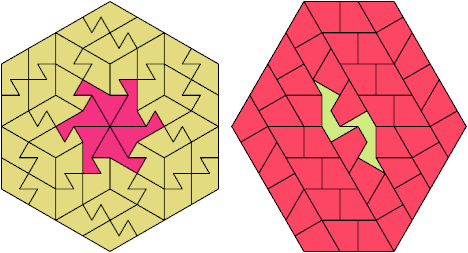
52 Tiles
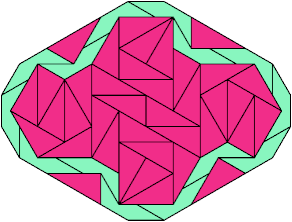
Lost Sheep
No convex pairing is known for any of these five tridrafters:
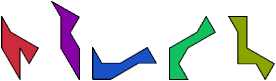
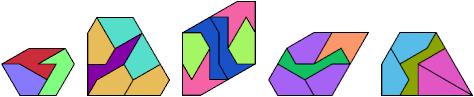
Each can form a convex shape with copies of two other tridrafters:
Last revised 2020-09-08.
Back to Polydrafter Tiling < Polyform Tiling < Polyform Curiosities
Col. George Sicherman [ HOME | MAIL ]